题目内容
【题目】如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
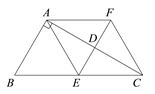
(1)求证:四边形AECF是菱形;
(2)若AB=10,∠ACB=30°,求菱形AECF的面积.
【答案】(1)证明见解析; (2)![]() .
.
【解析】(1)证明:∵ EF垂直平分AC,
∴ FA=FC,EA=EC,
∵ AF∥BC,
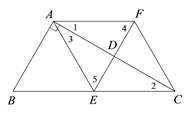
∴ ∠1=∠2.
∵ AE=CE,
∴ ∠2=∠3.
∴ ∠1=∠3.
∵ EF⊥AC,
∴ ∠ADF=∠ADE=90°.
∵ ∠1+∠4=90°,∠3+∠5=90°.
∴ ∠4=∠5.
∴ AF=AE.
∴ AF=FC=CE=EA.
∴ 四边形AECF是菱形.
(2)解:∵∠BAC=∠ADF=90°,
∴AB∥FE.
∵AF∥BE,
∴四边形ABEF为平行四边形.
∵AB=10,
∴FE=AB=10.
∵∠ACB=30°,
∴![]() .
.
∴![]() .
.

练习册系列答案
相关题目


