题目内容
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0), 点C(0,5),点D(1,8)在抛物线上,M为抛物线的顶点.求
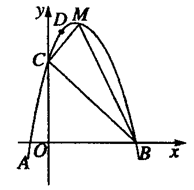
(1)抛物线的解析式;
(2)求△MCB的面积.
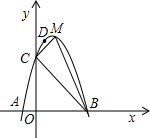

(1)抛物线的解析式;
(2)求△MCB的面积.

(1)y=-x2+4x+5.(2)15.
试题分析:(1)由A、C、D三点在抛物线上,根据待定系数可求出抛物线解析式;
(2)把BC边上的高和边长求出来,就可以得出面积.
(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
则有
0=a-b+c
5=c
8=a+b+c
解方程得a=-1,b=4,c=5所以抛物线解析式为y=-x2+4x+5.
(2)∵y=-x2+4x+5
=-(x-5)(x+1)
=-(x-2)2+9
∴M(2,9),B(5,0)
即BC=
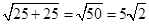 .
.由B、C两点坐标得直线BC的解析式为:l:x+y-5=0,
则点M到直线BC的距离为d=
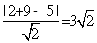 ,
,则S△MCB=
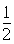 ×BC×d=15.
×BC×d=15.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (m是常数)
(m是常数)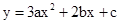 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;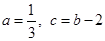 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;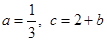 且抛物线在
且抛物线在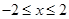 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.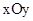 中,抛物线
中,抛物线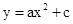 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0,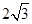 ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
 DB.
DB.

 ),当t =4秒时:
),当t =4秒时:
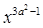 是关于x的二次函数,则a=_______.
是关于x的二次函数,则a=_______.