题目内容
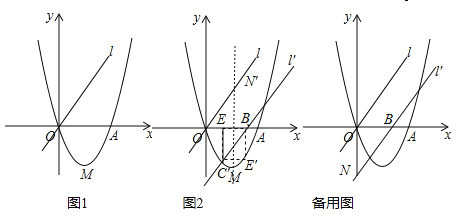
【题目】如图1，已知二次函数
（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为
，直线l的解析式为y=x．
（1）求二次函数的解析式；
（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；
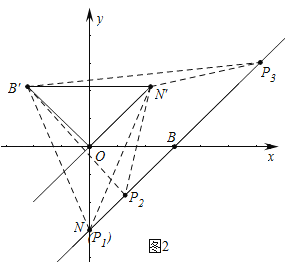
（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．
【答案】（1）
；（2）y=x﹣3；（3）P坐标为（0，﹣3）或（
，
）或（
，
）．
【解析】
试题分析：（1）由题意抛物线的顶点坐标为（2，
），设抛物线的解析式为
，把（0，0）代入得到a=
，即可解决问题；
（2）如图1中，设E（m，0），则C（m，
），B（
，0），由E、B关于对称轴对称，可得
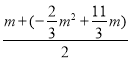=2，由此即可解决问题；
（3）分两种情形求解即可①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．②当N′=N′B′时，设P（m，m﹣3），列出方程解方程即可；
试题解析：（1）由题意抛物线的顶点坐标为（2，），设抛物线的解析式为，把（0，0）代入得到a=，∴抛物线的解析式为
，即．
（2）如图1中，设E（m，0），则C（m，），B（，0），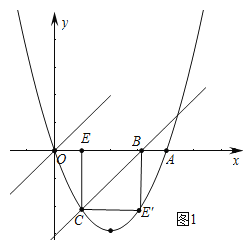
∵E′在抛物线上，∴E、B关于对称轴对称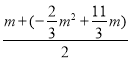，∴ =2，解得m=1或6（舍弃），∴B（3，0），C（1，﹣2），∴直线l′的解析式为y=x﹣3．
（3）如图2中，①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．
②当N′=N′B′时，设P（m，m﹣3），则有
，解得m=或，∴P2（，），P3（，）．
综上所述，满足条件的点P坐标为（0，﹣3）或（，）或（，）．
