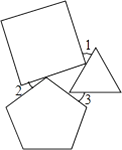
[题目]如图.DE⊥AB于E.DF⊥AC于F.若BD=CD.BE=CF.则下列结论:①DE=DF,②AD平分∠BAC,③AE=AD,④AB+AC=2AE中正确的是. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF，则下列结论：①DE=DF；②AD平分∠BAC；③AE=AD；④AB+AC=2AE中正确的是.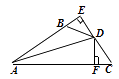

【答案】①、②、④
【解析】根据BE=CD，BE=CE，∠E=∠DFC=90°可得△BDE≌△CDF，则DE=DF，则①正确；
根据①可得AD平分∠BAC，则②正确；
根据角平分线可得∠EAD=∠FAD，∠D=∠AFD=90°，AD=AD可得△ADE≌△ADF，则AE=AF，则③错误；
根据①可得BE=FC，则AB+AC=AB+AF+CF=AB+BE+AF=AE+AF=2AE，则④正确.
故答案为：①、②、④.

可通过证明△BDE≌△CDF得出①；由△BDE≌△CDF可得②；再证明△ADE≌△ADF可得③；由AB+AC=AB+AF+CF=AB+BE+AF=AE+AF=2AE可证得④.

练习册系列答案

【题目】如图1，已知二次函数（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为，直线l的解析式为y=x．

（1）求二次函数的解析式；

（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；

（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．

【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F．

（1）求证：DE是⊙O的切线；

（2）若CF=2，DF=4，求⊙O直径的长．

【题目】下面是一位同学做的四道题：①2a+3b=5ab；②（3a3）2=6a6；③a6÷a2=a3；④a2a3=a5 ，其中做对的一道题的序号是（）
A.①
B.②
C.③
D.④

【题目】下列运算正确的是（）
A.a3+a3=a6
B.（a2）3=a5
C.a2a3=a5
D.a6÷a3=a2

【题目】数学课上林老师出示了问题：如图，AD∥BC，∠AEF=90°AD=AB=BC=DC，∠B=90°，点E是边BC的中点，且EF交∠DCG的平分线CF于点F，求证：AE=EF．
同学们作了一步又一步的研究：

（1）、经过思考，小明展示了一种解题思路：如图1，取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF，小明的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
（2）、小颖提出一个新的想法：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
（3）、小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．

【题目】如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．

（1）求抛物线的解析式；

（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；

（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．

【题目】将正三角形、正四边形、正五边形按如图所示的位置摆放．如果∠3=32°，那么∠1+∠2=度．

试题分类