题目内容
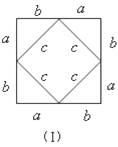
【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
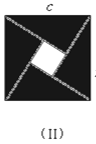
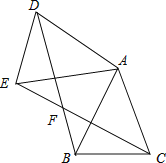
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
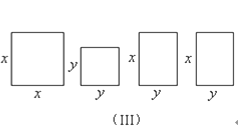
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)阴影部分面积由大正方形面积减去小正方形面积,也可以由四个直角三角形面积之和求出,两者相等即可得证;
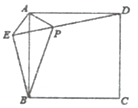
(2)拼成如图所示图形,根据大正方形边长为x+2y,表示出正方形面积,再由两个小正方形与两个矩形面积之和求出,即可验证.
试题解析:(1)S阴影=4×![]() ab,S阴影=c2-(a-b)2,
ab,S阴影=c2-(a-b)2,
∴4×![]() ab=c2-(a-b)2,即2ab=c2-a2+2ab-b2,
ab=c2-(a-b)2,即2ab=c2-a2+2ab-b2,
则a2+b2=c2;
(2)如图所示,

大正方形的面积为x2+4y2+4xy,也可以为(x+2y)2,
则(x+2y)2=x2+4xy+4y2.

练习册系列答案
相关题目