题目内容
【题目】如图，直线l1：y=x与双曲线y= 
相交于点A（a，2），将直线l1向上平移3个单位得到l2 ， 直线l2与双曲线相交于B、C两点（点B在第一象限），交y轴于D点． 
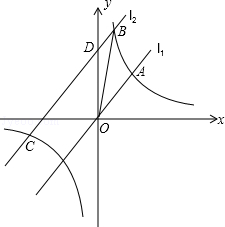
（1）求双曲线y= 的解析式；
（2）求tan∠DOB的值．
【答案】
（1）解：∵A（a，2）是y=x与y= 
的交点，
∴A（2，2），
把A（2，2）代入y= ，得k=4，
∴双曲线的解析式为y= 
（2）解：∵将l1向上平移了3个单位得到l2，
∴l2的解析式为y=x+3，
∴解方程组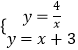 
，
得 
， 
，
∴B （1，4），
∴tan∠DOB= 
【解析】（1）由点A（a，2）在直线y=x上可知a=2，再代入y= 中求k的值即可；（2）将l1向上平移了3个单位得到l2的解析式为y=x+3，联立l2与双曲线解析式求交点B坐标，根据B点坐标，利用锐角三角函数定义求解．
【考点精析】根据题目的已知条件，利用锐角三角函数的定义的相关知识可以得到问题的答案，需要掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
