题目内容
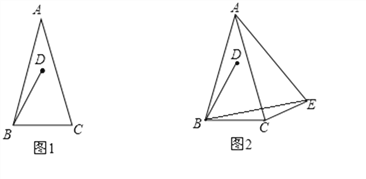
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),点D在△ABC内,且BD=BC,∠DBC=60°.
(1)如图1, 连接AD,直接写出∠ABD的度数(用含α的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
【答案】(1)30°- ![]() ;(2) △ABE是等边三角形,证明见解析;(3)30°.
;(2) △ABE是等边三角形,证明见解析;(3)30°.
【解析】试题分析:(1)求出∠ABC的度数,即可求出答案;
(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°-![]() α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=
α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() α,求出∠BEC=
α,求出∠BEC=![]() α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;
α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;
(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°-![]() α=15°,求出即可.
α=15°,求出即可.
试题解析:(1)(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() α,
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-![]() α;
α;
(2)△ABE是等边三角形,理由如下:
连接AD,CD,
∵∠ABE=60°, ∠ABD=30°- ![]() ,
,
∴∠DBE=30°+ ![]() ,
,
又∵∠DBC=60°,
∴∠CBE=30°- ![]() =∠ABD,
=∠ABD,
∵∠DBC=60°,BD=BC,
∴△BDC是等边三角形,
∴BD=CD,
在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,
∴∠BAD=∠CAD= ![]() ,
,
在△BCE中,∠BCE=150°,∠CBE=30°- ![]() ,
,
∴∠BEC= ![]() =∠BAD,
=∠BAD,
在△ABD和△CBE中, ∠BEC=∠BAD, ∠CBE=∠ABD,AB=AC,
∴△ABD≌△CBE,
∴AB=BE,
又∵∠ABE=60°,
∴△ABE是等边三角形;
(3)由(2)知△BDC是等边三角形,
∴∠BCD=60°,
∵∠BCE=150°,
∴∠DCE=90°,
∵∠DEC=45°,
∴△DCE是等腰直角三角形,
∴CD=CE=BC,在△BCE中, ∠BCE=150°,
∴∠CBE=30°- ![]() =15°,
=15°,
∴a=30°.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案




