题目内容
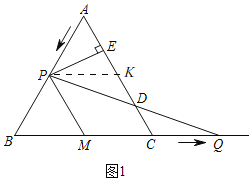
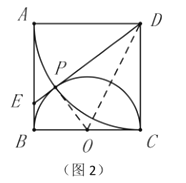
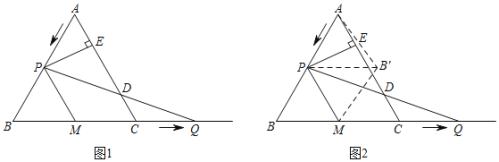
【题目】如图1，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动，动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s），过点P作PE⊥AC于E，PQ交AC边于D，线段BC的中点为M，连接PM．
（1）当t为何值时，△CDQ与△MPQ相似；
（2）在点P、Q运动过程中，点D、E也随之运动，线段DE的长度是否会发生变化？若发生变化，请说明理由，若不发生变化，求DE的长；
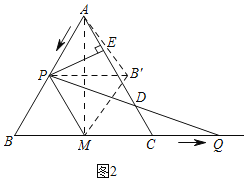
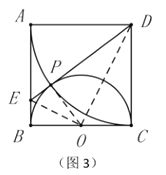
（3）如图2，将△BPM沿直线PM翻折，得△B'PM，连接AB'，当t为何值时，AB'的值最小？并求出最小值．
【答案】（1）t＝3时，△PMQ∽△DCQ；（2）不变化．DE＝3cm；（3）t为9﹣3
时，AB'的值最小，最小值为3﹣3．
【解析】
（1）根据等边三角形的性质可得∠B＝∠C＝60°，然后判断出相似三角形的对应关系可得PM∥DC，即可得出P是AB的中点，从而求出结论；
（2）P是AB的中点，根据等边三角形的性质和判定证出△APK是等边三角形，利用AAS证出△PKD≌△QCD，从而证出DK＝DC，即可求出结论；
（3）连接AM，易知当A，B'，M在一条直线上时，AB'最小，利用三线合一和勾股定理求出∠BAM和AM，即可求出AB'的最小值，由折叠知，BP＝B'P，∠PB'M＝∠B＝60°，最后根据AB'＝B'P即可求出结论．
解：（1）∵△ABC是等边三角形，
∴∠B＝∠C＝60°，
∴∠DBQ＝120°，
∵∠BQP＝∠CQD，∠PMQ＞90°，
∴只有当∠PMQ＝∠DCQ＝120°时，△PMQ∽△DCQ，
则PM∥DC，
∵M是BC的中点，
∴P是AB的中点，
即AP＝3＝t，
∴t＝3时，△PMQ∽△DCQ；
（2）不变化．理由如下：
如图1中，作PK∥BC交AC于K．
∵△ABC是等边三角形，
∴∠B＝∠A＝60°，
∵PK∥BC，
∴∠APK＝∠B＝60°，
∴△APK是等边三角形，
∴PA＝PK，
∵PE⊥AK，
∴AE＝EK，
∵AP＝CQ＝PK，∠PKD＝∠DCQ，∠PDK＝∠QDC，
∴△PKD≌△QCD（AAS），
∴DK＝DC，
∴DE＝EK+DK＝
（AK+CK）＝AC＝3cm；
（3）如图2中，连接AM，
则AB'≥AM﹣MB'，
而MB'＝MB，
∴当A，B'，M在一条直线上时，AB'最小，
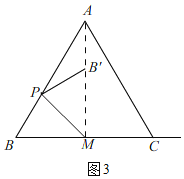
即：点B'在AM上，（如图3）
∵BM＝CM＝3，AB＝AC＝6，
∴AM⊥BC，
∴∠BAM＝∠BAC＝30°，
，
∵B'M＝BM＝3，
∴AB'的最小值为AM﹣B'M＝
，
由折叠知，BP＝B'P，∠PB'M＝∠B＝60°，
∴∠APB'＝∠PB'M﹣∠BAC＝30°＝∠BAM，
∴AB'＝B'P＝6﹣t＝3﹣3，
∴t＝9﹣3，
即：t为9﹣3时，AB'的值最小，最小值为3﹣3．
