题目内容
如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)求线段AD所在直线的函数表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A?D?C?B?A的 顺序在菱形的边上匀速运动一周,设运动时间为t秒、求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切.
顺序在菱形的边上匀速运动一周,设运动时间为t秒、求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切.
(1)求线段AD所在直线的函数表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A?D?C?B?A的
 顺序在菱形的边上匀速运动一周,设运动时间为t秒、求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切.
顺序在菱形的边上匀速运动一周,设运动时间为t秒、求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切.(1)∵点A的坐标为(-2,0),∠BAD=60°,∠AOD=90°,
∴OD=OA•tan60°=2
,
∴点D的坐标为(0,2
),(1分)
设直线AD的函数表达式为y=kx+b,
,
解得
.
∴直线AD的函数表达式为y=
x+2
.(3分)
(2)∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4,(5分)
如图所示: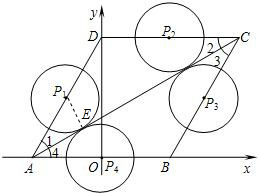
①点P在AD上与AC相切时,
连接P1E,则P1E⊥AC,P1E=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2.(6分)
②点P在DC上与AC相切时,
CP2=2r=2,
∴AD+DP2=6,
∴t2=6.(7分)
③点P在BC上与AC相切时,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10.(8分)
④点P在AB上与AC相切时,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切.(9分)
∴OD=OA•tan60°=2
| 3 |
∴点D的坐标为(0,2
| 3 |
设直线AD的函数表达式为y=kx+b,
|
解得
|
∴直线AD的函数表达式为y=
| 3 |
| 3 |
(2)∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4,(5分)
如图所示:

①点P在AD上与AC相切时,
连接P1E,则P1E⊥AC,P1E=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2.(6分)
②点P在DC上与AC相切时,
CP2=2r=2,
∴AD+DP2=6,
∴t2=6.(7分)
③点P在BC上与AC相切时,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10.(8分)
④点P在AB上与AC相切时,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切.(9分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 .
.