题目内容
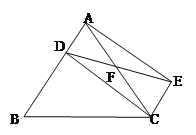
【题目】如图,点A在CB的延长线上,点F在DE的延长线上,连接AF,分别与BD、CE交于点G、H。已知∠1=52°,∠2=128°。
(1)求证:BD∥CE;
(2)若∠A=∠F,试判断∠C与∠D的数量关系,并说明理由。

【答案】(1)证明见解析;(2)∠C=∠D,理由见解析.
【解析】
(1)根据对顶角相等得出∠DGH的度数,再由平行线的判定定理即可得出结论;
(2)先根据BD∥CE得出∠D=∠CEF,再由∠A=∠F得出AC∥DF,据此可得出结论.
(1)证明:∵∠1=∠DGH=52°,∠2=128°,
∴∠DGH+∠2=180°,
∴BD∥CE;
(2)解:∠C=∠D.
理由:∵BD∥CE,
∴∠D=∠CEF.
∵∠A=∠F,
∴AC∥DF,
∴∠C=∠CEF,
∴∠C=∠D.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目