题目内容
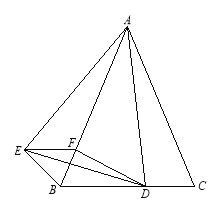
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为__.

【答案】2![]()
【解析】延长DE至H,使GH=BG,连接BH、CH,∵四边形ABCD为菱形,∴BC=DC=AB=BD,∴△BDC是等边三角形,∴∠DBC=∠BCF=60°,∵CE=DF,∴BC﹣CE=CD﹣DF,即BE=CF,在△DBE和△BCF中,∵DB=BC,∠DBC=∠BCF,BE=CF,∴△DBE≌△BCF(SAS),∴∠BDG=∠FBC,∴∠BDG+∠DBF=∠FBC+∠DBF=60°,∴∠BGE=∠BDG+∠DBF=60°,∴△BGH为等边三角形,∴BG=BH=2,∠GBH=60°,∴∠DBF+∠FBC=∠HBC+∠FBC,∴∠DBF=∠HBC,在△BGD和△BHC中,∵BD=BC,∠DBF=∠HBC,BG=BH,∴△BGD≌△BHC(SAS),∴DG=CH=4,∵∠FBC=∠BDG=∠BCH,∴BF∥CH,∴△BGE∽△CEH,∴ ![]() ,∵EG+EH=2,∴EG=
,∵EG+EH=2,∴EG=![]() ,∴BF=DE=4+
,∴BF=DE=4+![]() =
=![]() ,∵∠FBC=∠FBC,∠BGE=∠BCD=60°,∴△BGE∽△BCF,∴
,∵∠FBC=∠FBC,∠BGE=∠BCD=60°,∴△BGE∽△BCF,∴![]() ,∴
,∴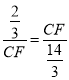 ,∴CF2=
,∴CF2=![]() ,CF=
,CF=![]() ,∴BE=CF=
,∴BE=CF=![]() ,∴BC=3BE=3×
,∴BC=3BE=3×![]() =
=![]() ,∴CD=BC=
,∴CD=BC=![]() .
.
故答案为: ![]() .
.


练习册系列答案
相关题目