题目内容
【题目】如图，已知二次函数y=ax2+ 
的图象与y轴交于点A（0，4），与x轴交于点B，C，点C坐标为（8，0），连AB，AC，点N在线段BC上运动（不与点B，C重合）过点N作NM∥AC，交AB于点M．
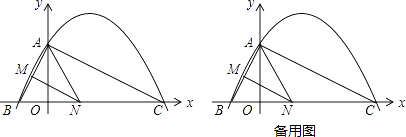
（1）判断△ABC的形状，并说明理由；
（2）当以点A，M，N为顶点的三角形与以点A，B，O为顶点的三角形相似时，求点N的坐标；
（3）当△AMN面积等于3时，直接写出此时点N的坐标．
【答案】
（1）
解：∵图象与y轴交于点A（0，4），
∴m=4．把点C的坐标代入函数解析式，得a=﹣ 
．
二次函数解析式为y=﹣ x2+ 
x+4．
当y=0时，﹣ x2+ x+4=0，解得x=8，x=﹣2．
∴点B的坐标为（﹣2，0）．
∴AB2=BO2+AO2=20，AC2=AO2+OC2=80．
∵BC2=（BO+OC）2=100，
在△ABC中，AB2+AC2=BC2．
∴△ABC是直角三角形
（2）
解：设点N的坐标为（n，0），则BN=n+2，
∵∠AOB=∠NMA=90°，
∴有两种情况．
①当 
= 
= 
时，易得∠BAO=∠ANM=∠BNM．
∴NB=NA，
∴BN2=NA2，
即（n+2）2=n2+42，解得n=3，此时N（3，0），
②当 = 
=2时，d点N与原点O重合，
∴此时N（0，0）
（3）
解：设点N的坐标为（n，0），﹣2＜n＜8，则BN=n+2，
过M点作MD⊥x轴于点D，
，
∵MD∥OA，∴△BMD∽△BAO，
∴ 
= 
．
∵MN∥AC， = 
，
∴ = ．
∵OA=4，BC=10，BN=n+2，
∴MD= 
（n+2）．
∵S△AMN=S△ABN﹣S△BMN=﹣ 
（n﹣3）2+5=3，
解得n=3 
，
∴N点坐标为（3+ 
，0）（3﹣ ，0）
【解析】（1）根据待定系数法可得函数解析式，根据自变量与函数值的对应关系，可得B点坐标，根据勾股定理及逆定理，可得答案；（2）根据相似三角形的性质，可得 = = ，根据BN与AN的关系，可得n，可得答案；（3）根据相似三角形的判定与性质，等量代换，可得， = ，可得MD，根据面积的和差，可得n的值，可得答案．
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本，需要知道一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
