Question

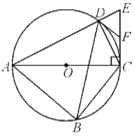
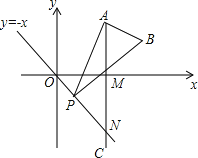
【题目】如图，已知点A是第一象限内横坐标为的一个定点，AC⊥x轴于点M，交直线y＝﹣x于点N．若点P是线段ON上的一个动点，∠APB＝30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是_____．

Answer 1

【答案】．

【解析】

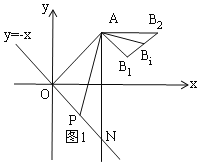
首先，需要证明线段B1B2就是点B运动的路径（或轨迹），如图1所示．利用相似三角形可以证明；其次，证明△APN∽△AB1B2，列比例式可得B1B2的长．

解：如图1所示，当点P运动至ON上的任一点时，设其对应的点B为Bi，连接AP，ABi，BBi，

∵AO⊥AB1，AP⊥ABi，

∴∠OAP＝∠B1ABi，

又∵AB1＝AOtan30°，ABi＝APtan30°，

∴AB1：AO＝ABi：AP，

∴△AB1Bi∽△AOP，

∴∠B1Bi＝∠AOP．

同理得△AB1B2∽△AON，

∴∠AB1B2＝∠AOP，

∴∠AB1Bi＝∠AB1B2，

∴点Bi在线段B1B2上，即线段B1B2就是点B运动的路径（或轨迹）．

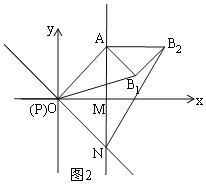
由图形2可知：Rt△APB1中，∠APB1＝30°，

∴

Rt△AB2N中，∠ANB2＝30°，

∴

∴

∵∠PAB1＝∠NAB2＝90°，

∴∠PAN＝∠B1AB2，

∴△APN∽△AB1B2，

∴，

∵ON：y＝﹣x，

∴△OMN是等腰直角三角形，

∴OM＝MN＝，

∴PN＝，

∴B1B2＝，

综上所述，点B运动的路径（或轨迹）是线段B1B2，其长度为．

故答案为：．