Question

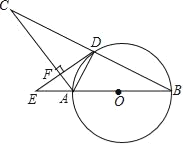
【题目】如图，在等腰△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D且BD＝2AD，过点D作DE⊥AC交BA延长线于点E，垂足为点F．

（1）求tan∠ADF的值；

（2）证明：DE是⊙O的切线；

（3）若⊙O的半径R＝5，求EF的长．

Answer 1

【答案】（1）；（2）见解析；（3）

【解析】

(1) AB是⊙O的直径，AB=AC，可得∠ADB=90°，∠ADF=∠B，可求得tan∠ADF的值；

（2）连接OD，由已知条件证明AC∥OD，又DE⊥AC，可得DE是⊙O的切线；

(3)由AF∥OD，可得△AFE∽△ODE，可得后求得EF的长．

解：（1）∵AB是⊙O的直径，

∴∠ADB=90°，

∵AB=AC，

∴∠BAD=∠CAD，

∵DE⊥AC，

∴∠AFD=90°，

∴∠ADF=∠B，

∴tan∠ADF=tan∠B==；

（2）连接OD，

∵OD=OA，

∴∠ODA=∠OAD，

∵∠OAD=∠CAD，

∴∠CAD=∠ODA，

∴AC∥OD，

∵DE⊥AC，

∴OD⊥DE，

∴DE是⊙O的切线；

（3）设AD=x，则BD=2x，

∴AB=x=10，

∴x=2，

∴AD=2，

同理得：AF=2，DF=4，

∵AF∥OD，

∴△AFE∽△ODE，

∴，

∴=，

∴EF=．