题目内容
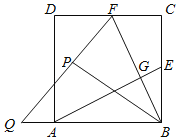
【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,点G,H在对角线BD上,且BG=DH.
(1)求证:△BFH≌△DEG;
(2)连接DF,若DF=BF,则四边形EGFH是什么特殊四边形?证明你的结论.

【答案】(1)见解析;(2)四边形EGFH是菱形,见解析.
【解析】
(1)证∠FBH=∠EDG,DE=BF,BH=DG,由SAS即可得出结论;
(2)连接EF交GH于O,由全等三角形的性质得出FH=EG,∠BHF=∠DGE,证出FH∥EG,得出四边形EGFH是平行四边形,由等腰三角形的性质得出EF⊥GH,即可得出四边形EGFH是菱形.
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠FBH=∠EDG,
∵AE=CF,BG=DH,
∴DE=BF,BH=DG,
在△BFH和△DEG中,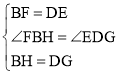 ,
,
∴△BFH≌△DEG(SAS);
(2)解:若DF=BF,则四边形EGFH是菱形;理由如下:
连接EF交GH于O,如图:
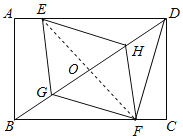
由(1)得:△BFH≌△DEG,
∴FH=EG,∠BHF=∠DGE,
∴FH∥EG,
∴四边形EGFH是平行四边形,
∴OG=OH,
∵BG=DH,
∴OB=OD,
∵DF=BF,
∴EF⊥GH,
∴四边形EGFH是菱形.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目