题目内容
【题目】如图,在平面直角坐标系内,点A,B的坐标分别为(1,0),(0,2),AC⊥AB,且AB=AC,直线BC交![]() 轴于点D,抛物线
轴于点D,抛物线![]() 经过点A,B,D.
经过点A,B,D.

(1)求直线BC和抛物线![]() 的函数表达式;
的函数表达式;
(2)点P是直线BD下方的抛物线上一点,求△PCD面积的最大值,以及△PCD面积取得最大值时,点P的坐标;
(3)若点P的坐标为(2)小题中,△PCD的面积取得最大值时对应的坐标.平面内存在直线l,使点B,D,P到该直线的距离都相等,请直接写出所有满足条件的直线l的函数表达式.
【答案】(1)![]() ,
,![]() ;(2)△PCD的面积最大值为
;(2)△PCD的面积最大值为![]() ,P(3,
,P(3,![]() );(3)
);(3)![]() ,
,![]() ,
,![]()
【解析】
(1)如下图,先求出点C的坐标,从而求得BC的解析式,进而得出点D的坐标,从而得出抛物线的解析式;
(2)如下图,设点P的横坐标为![]() ,
,![]() ,将△PCD的面积用t表示出来,利用二次函数的性质求出最大值;
,将△PCD的面积用t表示出来,利用二次函数的性质求出最大值;
(3)存在三条直线,分别是△PDB三条中位线所在的直线.
解:(1)过点C作CE⊥![]() 轴,垂足为E.
轴,垂足为E.
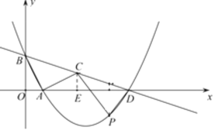
∵AB=AC,∠AOB=∠CEA=90°,∠ABO=∠CAE,
∴△ABO≌△CAE.
∴AO=CE,BO=AE.
∵A(1,0),B(0,2),∴CE=AO=1,AE=BO=2.
∴C(3,1).
设直线BC的函数表达式为![]() (
(![]() ).
).
把点B(0,2),C(3,1)代入,得
![]() 解方程组,得
解方程组,得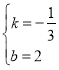
所以,直线BC的函数表达式为![]() .
.
令![]() ,得
,得![]() ,
,
∴D(6,0).
∵抛物线![]() 经过点A(1,0),D (6,0).
经过点A(1,0),D (6,0).
∴![]() 解方程组,得
解方程组,得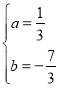
∴抛物线的函数表达式为![]() .
.
(2)过点P作![]() 轴的垂线,垂足为H,交BD于点F.令P的横坐标为
轴的垂线,垂足为H,交BD于点F.令P的横坐标为![]() .
.
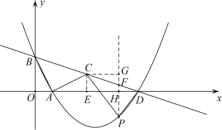
∵点P在BD直线下方的抛物线上移动,
∴PF=![]() .
.
过点C作CG⊥PF,垂足为G.
![]()
![]() .
.
所以,当![]() 时,△PCD的面积取得最大值,最大值为
时,△PCD的面积取得最大值,最大值为![]() .
.
此时点P坐标为(3,![]() ).
).
(3)满足条件的直线有三条,是△PDB三条中位线所在的直线.
图形如下图,点I、J、K分别是BP、BD和PD的中点
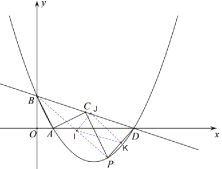
∵P(3,-2),B(0,2),D(6,0)
∴I(![]() ,0),J(3,1),K(
,0),J(3,1),K(![]() ,-1)
,-1)
∴IJ所对应的直线解析式为:![]()
IK所对应的直线解析式为:![]()
JK所对应的直线解析式为:![]()
综上得:三条直线的函数表达式分别为![]() ,
,![]() ,
,![]() .
.

 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】下列数据是甲、乙、丙三人各10轮投篮的得分(每轮投篮10次,每次投中记1分):
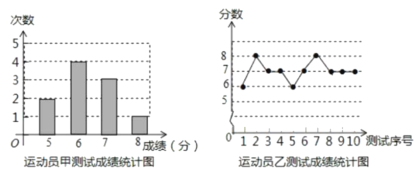
丙得分的平均数与众数都是7,得分统计表如下:
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力,你认为选谁更合适?请用你所学过的统计知识加以分析说明(参考数据:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之间进行传球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,经过三次传球后球又回到乙手中的概率是多少?(用树状图或列表法解答)