题目内容
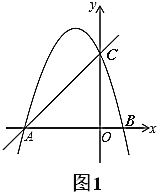
【题目】如图,在平面直角坐标系中,一次函数![]()
![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
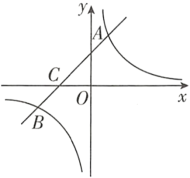
(1)求该反比例函数和一次函数的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
【答案】(1)反比例函数解析式:y2=![]() ;一次函数的解析式:y1=x+2(2)
;一次函数的解析式:y1=x+2(2)![]() 的最大值
的最大值![]() ,点
,点![]() 的坐标(0,2).
的坐标(0,2).
【解析】
(1)把A(3,5)代入y2=![]() (m≠0),可求出反比例函数的关系式,求出点B坐标,进而确定一次函数关系式;
(m≠0),可求出反比例函数的关系式,求出点B坐标,进而确定一次函数关系式;
(2)求出一次函数与y轴的交点坐标,可得此时PB-PC最大,为BC,根据勾股定理求出结果即可.
解:解:(1)把A(3,5)代入y2=![]() (m≠0),可得m=3×5=15,
(m≠0),可得m=3×5=15,
∴反比例函数的解析式为y2=![]() ;
;
把点B(a,-3)代入y2=![]() ,可得a=-5,
,可得a=-5,
∴B(-5,-3).
把A(3,5),B(-5,-3)代入y1=x+b,可得
![]() ,
,
解得
![]() ,
,
∴一次函数的解析式为y1=x+2;
(2)一次函数的解析式为y1=x+2,令x=0,则y=2,
∴一次函数与y轴的交点为P(0,2),
此时,PB-PC=BC最大,P即为所求,
令y=0,则x=-2,
∴C(-2,0),
∴BC=![]() .
.
综上所述,![]() 的最大值
的最大值![]() ,点
,点![]() 的坐标(0,2).
的坐标(0,2).

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目