Question

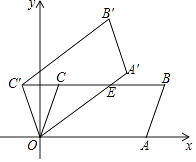
【题目】已知：四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点（与C、D不重合）,将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.

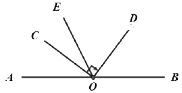
（1）如图1,∠AEE'= °;

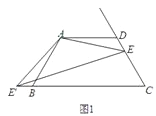
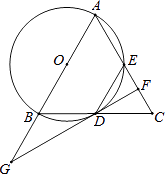
（2）如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;

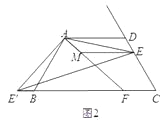
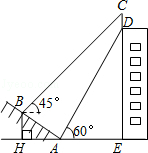
（3）如图3,在（2）的条件下,如果CE=2,AE=,求ME的长.

Answer 1

【答案】(1)∠AEE'=30°;

(2)当点E在线段CD上时,;

当点E在CD的延长线上时,

时,;

时,;

时,;

(3)．

【解析】

试题（1）根据旋转地的性质易得到△ADE≌△ABE/,∠EAE/=120°，所以∠AEE/=30°.

由于点E是射线CD上一动点，其位置不确定，故应分情况讨论：一是当点E在线段CD上时：此时易得；二是点E在CD的延长线上时，仍需考虑多种情况，可以知道，当∠EAD=300时，AE旋转后的直线与BC平行，当∠EAD=900时，AE旋转后的直线与AB共线，而∠EAD不可能为1200，所以应再次细分为三种情况：即当时；当时；当时.

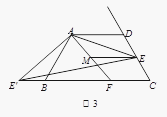
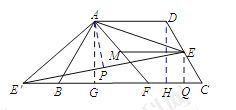
(3）如图，作于点G, 作于点H.易知四边形AGHD是矩形和两个全等的直角三角形；∴点、B、C在一条直线上.继续作于Q.于点P. 多次利用勾股定理可得，，；继而证明Rt△AG E'∽Rt△FA E'，根据相似三角形性质可求解.

试题解析：

解：(1) 30°.

当点E在线段CD上时，；

当点E在CD的延长线上，

时，；

时，；

时，.

(3)作于点G, 作于点H.

由AD∥BC，AD=AB=CD，∠BAD=120°，得∠ABC=∠DCB=60°，

易知四边形AGHD是矩形和两个全等的直角三角形.则GH="AD" , BG=CH.

∵,

∴点、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=,.

作于Q.在Rt△EQC中，CE="2,",

∴,.

∴E'Q=.

作于点P.

∵△ADE绕点A顺时针旋转120°后，得到△ABE'.

∴△A EE'是等腰三角形，.

∴在Rt△AP E'中，E'P=.

∴EE'="2" E'P=.

∴在Rt△EQ E'中，E'Q=.

∴.

∴.

∴，.

∴

在Rt△E'AF中,

∴Rt△AG E'∽Rt△FA E'.

∴

∴.

∴.

由（2）知：.

∴.