题目内容
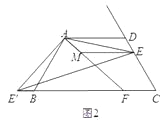
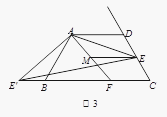
【题目】如图,矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转90°,点B、D分别落在点B′,D′处,且点A,B′,D′在同一直线上,则tan∠DAD′ . 
【答案】![]()
【解析】解:由题意可得:AD∥CD′, 故△ADE∽△D′CB′,
则 ![]() =
= ![]() ,
,
设AD=x,则B′C=x,DB′=4﹣x,AB=CD′=4,
故 ![]() =
= ![]() ,
,
解得:x1=﹣2﹣2 ![]() (不合题意舍去),x2=﹣2+2
(不合题意舍去),x2=﹣2+2 ![]() ,
,
则DB′=6﹣2 ![]() ,
,
则tan∠DAD′= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用矩形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目