题目内容
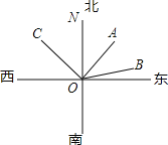
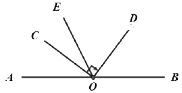
【题目】已知点A、O、B在一条直线上,将射线OC绕O点顺时针方向旋转90°后,得到射线OD,在旋转过程中,射线OC始终在直线AB上方,且OE平分∠AOD.约定,无论∠AOD大小如何,OE都看作是由OA、OD两边形成的最小角的平分线.
(1)如图,当∠AOC=30°时,∠BOD=_________°;
(2)若射线OF平分∠BOC,求∠EOF的度数.
【答案】(1)60;(2)45°或135°
【解析】
(1)根据平角定义即可得出结论;
(2)分两种情况讨论:①当OC、OD都在直线AB上方时;当OC在直线AB上方,OD在直线AB下方时.
(1)∵∠AOC=30°,∠COD=90°,∴∠BOD=180°-∠AOC-∠COD=180°-30°-90°=60°.
(2)分两种情况讨论:
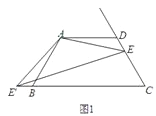
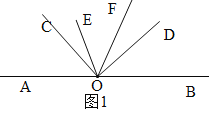
①当OC、OD都在直线AB上方时,如图1.设∠AOC=x,则∠BOC=180°-x.
∵∠COD=90°,∴∠AOD=90°+x,∠BOD=90°-x.
∵OE平分∠AOD,∴∠EOD=![]() ∠AOD=
∠AOD=![]() (90°+x)=45°+0.5x.
(90°+x)=45°+0.5x.
∵OF平分∠BOC,∴∠BOF=![]() ∠BOC=
∠BOC=![]() (180°-x)=90°-0.5x,∴∠FOD=∠BOF-∠BOD=(90°-0.5x)-(90°-x)=0.5x,∴∠EOF=∠EOD-∠DOF=(45°+0.5x)-0.5x=45°.
(180°-x)=90°-0.5x,∴∠FOD=∠BOF-∠BOD=(90°-0.5x)-(90°-x)=0.5x,∴∠EOF=∠EOD-∠DOF=(45°+0.5x)-0.5x=45°.
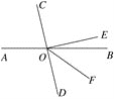
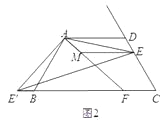
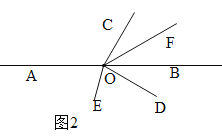
②当OC在直线AB上方,OD在直线AB下方时,如图2.
设∠AOC=x,则∠BOC=180°-x.
∵∠COD=90°,∴∠AOD=360°-90°-x=270°-x,∠BOD=180°-∠AOD=180°-(270°-x)=x-90°.
∵OE平分∠AOD,∴∠EOD=![]() ∠AOD=
∠AOD=![]() (270°-x)=135°-0.5x.
(270°-x)=135°-0.5x.
∵OF平分∠BOC,∴∠BOF=![]() ∠BOC=
∠BOC=![]() (180°-x)=90°-0.5x,∴∠FOD=∠BOF+∠BOD=(90°-0.5x)+(x-90°)=0.5x,∴∠EOF=∠EOD+∠DOF=(135°-0.5x)+0.5x=135°.
(180°-x)=90°-0.5x,∴∠FOD=∠BOF+∠BOD=(90°-0.5x)+(x-90°)=0.5x,∴∠EOF=∠EOD+∠DOF=(135°-0.5x)+0.5x=135°.
综上所述:∠EOF的度数为45°或135°.

【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.