题目内容
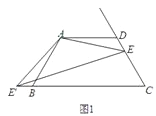
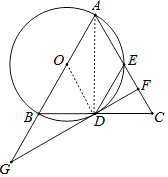
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E.过点D作⊙O的切线,交AC于点F,交AB的延长线于点G,连接DE. 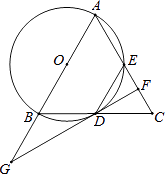
(1)求证:BD=CD;
(2)若∠G=40°,求∠AED的度数.
(3)若BG=6,CF=2,求⊙O的半径.
【答案】
(1)证明:连接AD,
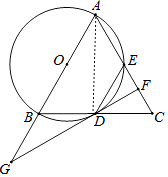
∵AB为直径,
∴∠ACB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD
(2)解:连接OD,
∵GF是切线,OD是半径,
∴OD⊥GF,
∴∠ODG=90°,
∵∠G=40°,
∴∠GOD=50°,
∵OB=OD,
∴∠OBD=65°,
∵点A、B、D、E都在⊙O上,
∴∠ABD+∠AED=180°,
∴∠AED=115°
(3)解:∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△GOD∽△GAF,
∴ ![]() =
= ![]() ,
,
∴设⊙O的半径是r,则AB=AC=2r,
∴AF=2r﹣2,
∴ ![]() =
= ![]() ,
,
∴r=3,
即⊙O的半径是3
【解析】(1)连接AD,根据圆周角定理得出AD⊥BC,根据等腰三角形的性质得出即可;(2)连接OD,根据切线的性质求出∠ODG=90°,求出∠BOD、∠ABC,根据圆内接四边形求出即可;(3)求出△ODG∽△AFG,得出比例式,即可求出圆的半径.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 阅读快车系列答案
阅读快车系列答案【题目】在一次“探究性学习”课中,李老师设计了如下数表:
n | 2 | 3 | 4 | 5 | … |
a | 22﹣1 | 32﹣1 | 42﹣1 | 52﹣1 | … |
b | 4 | 6 | 8 | 10 | … |
c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)用含自然数n(n>1)的代数式表示:a,b,c.
(2)当c=101时,求n的值;
(3)用等式表示a、b、c之间的数量关系