题目内容
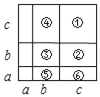
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )

A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
【答案】D
【解析】
通过几何图形面积之间的数量关系完全平方公式或其他等式作出几何解释即可.
依据①②③④四部分的面积可得,(b+c)2=b2+2bc+c2,故A能验证;
依据⑤⑥两部分的面积可得,a(b+c)=ab+ac,故B能验证;
依据整个图形的面积可得,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,故C能验证;
图中不存在长为a+2b,宽为a的长方形,故D选项不能验证;
故选:D.

练习册系列答案
相关题目