题目内容
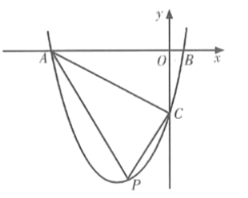
【题目】如图所示,抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
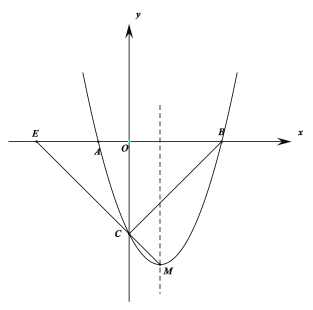
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接![]() 求
求![]() 面积的最大值及此时点N的坐标.
面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与![]() 相似.若存在,求出点P的坐标;若不存在,请说明理由.
相似.若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) (0,-3),(1,-4);(2) ![]() ,(
,(![]() );(3) G点坐标存在,为(2,-3)或(4,5)或(-2,5);(4) P点坐标存在,为
);(3) G点坐标存在,为(2,-3)或(4,5)或(-2,5);(4) P点坐标存在,为![]() 或
或![]() .
.
【解析】
(1)令抛物线解析式中x=0即可求出C点坐标,由公式![]() 即可求出顶点M坐标;
即可求出顶点M坐标;
(2)如下图所示,过N点作x轴的垂线交直线BC于Q点,设N(![]() ),求出BC解析式,进而得到Q点坐标,最后根据
),求出BC解析式,进而得到Q点坐标,最后根据![]() 即可求解;
即可求解;
(3)设D点坐标为(1,t),G点坐标为(![]() ),然后分成①DG是对角线;②DB是对角线;③DC是对角线时三种情况进行讨论即可求解;
),然后分成①DG是对角线;②DB是对角线;③DC是对角线时三种情况进行讨论即可求解;
(4)连接AC,由CE=CB可知∠B=∠E,求出MC的解析式,设P(x,-x-3),然后根据△PEO相似△ABC,分成![]() 和
和![]() 讨论即可求解.
讨论即可求解.
解:(1)令![]() 中x=0,此时y=-3,故C点坐标为(0,-3),
中x=0,此时y=-3,故C点坐标为(0,-3),
又二次函数的顶点坐标为![]() ,代入数据解得M点坐标为
,代入数据解得M点坐标为![]() ,
,
故答案为:C点坐标为(0,-3), M点坐标为(1,-4);
(2) 过N点作x轴的垂线交直线BC于Q点,连接BN,CN,如下图所示:
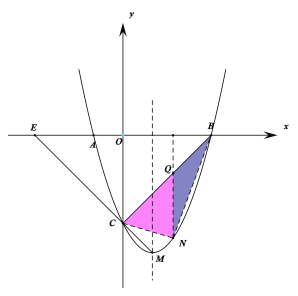
令![]() 中y=0,解得B(3,0),A(-1,0),
中y=0,解得B(3,0),A(-1,0),
设直线BC的解析式为:![]() ,代入C(0,-3),B(3,0),
,代入C(0,-3),B(3,0),
∴![]() ,解得
,解得![]() ,即直线BC的解析式为:
,即直线BC的解析式为:![]() ,
,
设N点坐标为(![]() ),故Q点坐标为
),故Q点坐标为![]() ,其中
,其中![]() ,
,
则![]()
![]()
![]() ,其中
,其中![]() 分别表示Q,C,B三点的横坐标,
分别表示Q,C,B三点的横坐标,
且![]() ,
,![]() ,
,
故![]() ,其中
,其中![]() ,
,
当![]() 时,
时,![]() 有最大值为
有最大值为![]() ,
,
此时N的坐标为(![]() ),
),
故答案为:![]() 有最大值为
有最大值为![]() ,N的坐标为(
,N的坐标为(![]() );
);
(3) 设D点坐标为(1,t),G点坐标为(![]() ),且B(3,0),C(0,-3)
),且B(3,0),C(0,-3)
分类讨论:
情况①:当DG为对角线时,则另一对角线是BC,由中点坐标公式可知:
线段DG的中点坐标为![]() ,即
,即![]() ,
,
线段BC的中点坐标为![]() ,即
,即![]() ,
,
此时DG的中点与BC的中点为同一个点,
故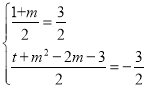 ,解得
,解得![]() ,
,
检验此时四边形DCGB为平行四边形,此时G坐标为(2,-3);
情况②:当DB为对角线时,则另一对角线是GC,由中点坐标公式可知:
线段DB的中点坐标为![]() ,即
,即![]() ,
,
线段GC的中点坐标为![]() ,即
,即![]() ,
,
此时DB的中点与GC的中点为同一个点,
故 ,解得
,解得![]() ,
,
检验此时四边形DCBG为平行四边形,此时G坐标为(4,5);
情况③:当DC为对角线时,则另一对角线是GB,由中点坐标公式可知:
线段DC的中点坐标为![]() ,即
,即![]() ,
,
线段GB的中点坐标为![]() ,即
,即![]() ,
,
此时DB的中点与GC的中点为同一个点,
故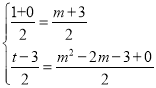 ,解得
,解得![]() ,
,
检验此时四边形DGCB为平行四边形,此时G坐标为(-2,5);
综上所述,G点坐标存在,为(2,-3)或(4,5)或(-2,5);
(4) 连接AC,OP,如下图所示,
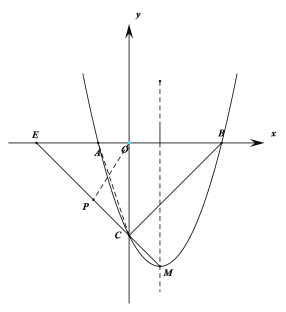
设MC的解析式为:y=kx+m,代入C(0,-3),M(1,-4)
即![]() ,解得
,解得![]()
∴MC的解析式为:![]() ,令
,令![]() ,求得E点坐标为(-3,0),
,求得E点坐标为(-3,0),
∴OE=OB=3,且OC=OC,
∴CE=CB,即∠B=∠E,
设P(x,-x-3),又∵P点在线段EC上,∴-3<x<0,
则![]() ,
,![]() ,
,
由题意知:△PEO相似△ABC,
分类讨论:
情况①:![]()
∴![]() ,解得
,解得![]() ,满足-3<x<0,此时P的坐标为
,满足-3<x<0,此时P的坐标为![]() ;
;
情况②:![]()
∴![]() ,解得
,解得![]() ,满足-3<x<0,此时P的坐标为
,满足-3<x<0,此时P的坐标为![]() .
.
综上所述,P点的坐标为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
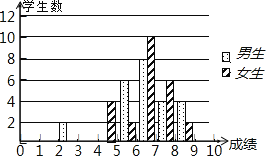
小学生10分钟应用题系列答案【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?