��Ŀ����
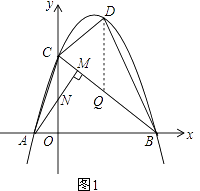
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��x�ᡢy��ֱ��ڵ�B��4��0����C��0��3������AΪx�Ḻ������һ�㣬AM��BC�ڵ�M��y���ڵ�N������4CN=5ON����֪������y=ax2+bx+c������A��B��C��
��1���������ߵĺ�����ϵʽ��
��2������AC����D���߶�BC�Ϸ����������ϣ�����DC��DB������BCD�͡�ABC�������S��BCD= ![]() S��ABC �� ���D�����ꣻ
S��ABC �� ���D�����ꣻ
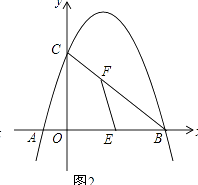
��3����ͼ2��EΪOB�е㣬��FΪ�߶�BC��һ�㣨�����˵㣩������EF��һ����P��E���������߶�EF��ÿ��1����λ���ٶ��˶���F���������߶�FC��ÿ�� ![]() ����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
���𰸡�
��1��
�⣺��C��0��3����
��OC=3��
��4CN=5ON��
��ON= ![]() ��
��
�ߡ�OAN=��NCM��
���AON�ס�COB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OA=1��
�����OA=1��
��A����1��0����
�������߽���ʽΪy=a��x+1����x��4����
��C��0��3�������a1����4��=3�����a=�� ![]() ��
��
�������߽���ʽΪy=�� ![]() ��x+1����x��4��=��
��x+1����x��4��=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��ֱ��BC�Ľ���ʽΪy=mx+n��
��C��0��3����B��4��0������� ![]() �����
�����  ��
��
��ֱ��BC�Ľ���ʽΪy=�� ![]() x+3��
x+3��
��PQ��y�ύBC��Q����ͼ1��
��P��x���� ![]() x2+
x2+ ![]() x+3������Q��x����
x+3������Q��x���� ![]() x+3����
x+3����
DQ=�� ![]() x2+
x2+ ![]() x+3������
x+3������ ![]() x+3��=��
x+3��=�� ![]() x2+3x��
x2+3x��
��S��BCD=S��CDQ+S��BDQ= ![]() 4����
4���� ![]() x2+3x��=��
x2+3x��=�� ![]() x2+6x��
x2+6x��
��S��BCD= ![]() S��ABC��
S��ABC��
�ੁ ![]() x2+6x=
x2+6x= ![]() ��
�� ![]() ����4+1����3��
����4+1����3��
������x2��4x+3=0�����x1=1��x2=3��
��D��������1�� ![]() ����3��3����
����3��3����
��3��
�⣺��F��m���� ![]() x+3������EF=
x+3������EF= ![]() =
= ![]() ��CF=
��CF= ![]() ��
��
��P�������˶�����������ʱ��t=EF+ ![]() =EF+
=EF+ ![]() CF��2
CF��2 ![]() ����EF=
����EF= ![]() CFʱ��ȡ�Ⱥţ���ʱt��С��
CFʱ��ȡ�Ⱥţ���ʱt��С��
�� ![]() x2��
x2�� ![]() x+13=��
x+13=�� ![]()
![]() x��2��
x��2��
������2x2��17x+26�����x1=2��x2= ![]() ����ȥ����
����ȥ����
���P�������˶����������õ�����ʱ��2�� ![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2�� ![]() ����
����
����������1��������OC=3��4CN=5ON�����ON= ![]() ����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A����1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=��
����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A����1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+3����2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��
x+3����2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=�� ![]() x+3����PQ��y�ύBC��Q����ͼ1����P��x����
x+3����PQ��y�ύBC��Q����ͼ1����P��x���� ![]() x2+
x2+ ![]() x+3������Q��x����
x+3������Q��x���� ![]() x+3�����ټ����DQ=��
x+3�����ټ����DQ=�� ![]() x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=��
x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=�� ![]() x2+6x��Ȼ�����S��BCD=
x2+6x��Ȼ�����S��BCD= ![]() S��ABC�õ���
S��ABC�õ��� ![]() x2+6x=
x2+6x= ![]() ��
�� ![]() ����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ��3����F��m����
����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ��3����F��m���� ![]() x+3�����������ľ��빫ʽ�õ�EF=
x+3�����������ľ��빫ʽ�õ�EF= ![]() ��CF=
��CF= ![]() x�����P�������˶�����������ʱ��t=EF+
x�����P�������˶�����������ʱ��t=EF+ ![]() =EF+
=EF+ ![]() CF�����ݲ���ʽ��ʽ�õ�EF+
CF�����ݲ���ʽ��ʽ�õ�EF+ ![]() CF��2
CF��2 ![]() ����EF=
����EF= ![]() CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��
CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ�� ![]() x2��
x2�� ![]() x+13=��
x+13=�� ![]()
![]() x��2��x1=2��x2=
x��2��x1=2��x2= ![]() ����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��
����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2�� ![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2�� ![]() ����
����

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�