题目内容
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
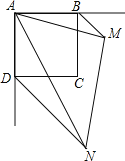
【答案】(1)证明见解析;(2)当∠BAM=22.5°时,四边形BMND为矩形,证明见解析.
【解析】分析:(1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
本题解析:(1)∵四边形ABCD是正方形,
∴∠DAB=∠ADC=∠ABC=90°,AB=AD.∵∠PAQ=45°∴∠1+∠2=45°,
∵ND平分∠FDC,MB平分∠EBC,∴∠EBM=∠FDN=45°,∴∠ABM=∠ADN=135°∠2+∠3=45° ,∴∠1=∠3 ∴△ABM∽△NDA
(2)当∠BAM=22.5°时,四边形BMND为矩形
理由:∵∠1=22.5°,∠EBM=45°∴∠4=22.5°,∴∠1=∠4,∴AB=BM
同理AD=DN∵AB=AD∴BM=DN ∵四边形ABCD是正方形∴∠ABD=∠ADB=45°
∴∠BDN=∠DBM=90°∴∠BDN+∠DBM=180°∴BM∥DN
∴四边形BMND为平行四边形
∵∠BDN=90°∴四边形BMND为矩形.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目


