题目内容
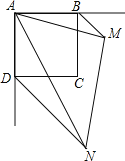
【题目】如图,平面直角坐标系xOy中,已知点A(0,3),点B(![]() ,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
,0),连接AB.若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
(1)在点C1(-2,![]() ),点C2(0,-2),点C3(
),点C2(0,-2),点C3(![]() ,
,![]() )中,线段AB的“等长点”是点 ;
)中,线段AB的“等长点”是点 ;
(2)若点D(m,n)是线段AB的“等长点”,且∠DAB=60°,求m和n的值;
(3)若直线![]() 上至少存在一个线段AB的“等长点”,直接写出k的取值范围.
上至少存在一个线段AB的“等长点”,直接写出k的取值范围.

【答案】(1)C1,C3 ;(2)m=![]() ,n=0或m=
,n=0或m=![]() ,n=3.(3)
,n=3.(3)![]()
【解析】分析:(1)直接利用线段AB的“等长点”的条件判断;
(2)分两种情况讨论,利用对称性和垂直的性质即可求出m,n;
(3)先判断出直线y=kx+3![]() 与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
与圆A,B相切时,如图2所示,利用相似三角形的性质即可求出结论
本题解析:
(1)C1,C3
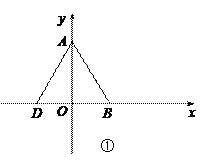
(2)如图①,∵点D(m,n)是线段AB的“等长点”,且∠DAB=60°,
∴△ABD是等边三角形.∵OA=3,
OB=![]() ,∠AOB=90°,∴tan∠ABO=
,∠AOB=90°,∴tan∠ABO=![]() ,
,
∴∠ABO=60°,∠BAO=30°,
∴点D在x轴上,且DB=AB=2![]() ,
,
∴m=-![]() ,n=0.
,n=0.
如图②,同理可知△ABD是等边三角形,∵∠DAB=60°,∠BAO=30°,∴∠DAO=90°,又∵DA=AB=2![]() ,
,
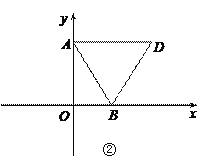 ∴m=2
∴m=2![]() ,n=3.
,n=3.
综上所述,m=-![]() ,n=0或m=2
,n=0或m=2![]() ,n=3.
,n=3.
(3)如图2,∵直线y=kx+3![]() k=k(x+3
k=k(x+3![]() ),
),
∴直线y=kx+3![]() k恒过一点P(3
k恒过一点P(3![]() ,0),
,0),
∴在Rt△AOP中,OA=3,OP=3![]() ,
,
∴∠APO=30°,
∴∠OPA=60°,
∴∠BAP=90°,
当PF与⊙B相切时交y轴于F,
∴PA切⊙B于A,
∴点F就是直线y=kx+33√k与⊙B的切点,
∴F(0,3),
∴33√k=3,
∴k=3√3,
当直线y=kx+3![]() k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
k与⊙A相切时交y轴于G切点为E,∴∠AEG=∠OPG=90°,
∴△AEG∽△POG,
∴![]() ,
,
∴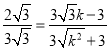 ,
,
∴k=![]() (舍)或k=
(舍)或k=![]() ,
,
∵直线y=kx+3![]() k上至少存在一个线段AB的“等长点”,
k上至少存在一个线段AB的“等长点”,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案