题目内容
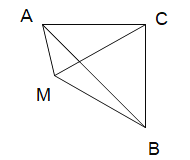
【题目】已知△ABC是等腰直角三角形,∠ACB=90°.
(1)如图,点M在斜边AB上,且AC=![]() ,MA=
,MA=![]() ,则线段MB=___________,MC=__________;
,则线段MB=___________,MC=__________;
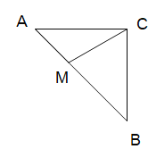
(2)如图,点M在![]() ABC外,MA=2,MC=5,∠AMC=45°,求MB;
ABC外,MA=2,MC=5,∠AMC=45°,求MB;
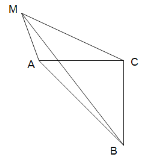
(3)如图,点M在![]() ABC外,MA=3,MB=
ABC外,MA=3,MB=![]() ,MC=6,求AC.
,MC=6,求AC.
【答案】(1)MB=![]() ,MC=2;(2)MB=
,MC=2;(2)MB=![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点C作![]() ,则
,则![]() 垂直平分
垂直平分![]() ,由△ABC是等腰直角三角形,可求得
,由△ABC是等腰直角三角形,可求得![]() 的长,进而求出
的长,进而求出![]() 的长,则
的长,则![]() 即可解得;
即可解得;
(2)过点C作CN⊥CM,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,由
,由![]() 可证得
可证得![]() 是等腰直角三角形,根据等腰三角形的性质可求出
是等腰直角三角形,根据等腰三角形的性质可求出![]() 的长,由△ABC是等腰直角三角形,可证得
的长,由△ABC是等腰直角三角形,可证得![]() ,进而证明
,进而证明![]() ,
,![]() ,再根据勾股定理即可求得
,再根据勾股定理即可求得![]() 的长;
的长;
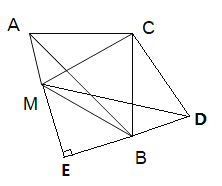
(3)过C作CD⊥CM且CD=CM,连接BD、MD,延长AM,DB交于E.根据等腰直角三角形的性质可证得![]() 进而证明
进而证明![]() 是直角三角形, 设
是直角三角形, 设![]() ,
,
求出![]() ,再根据勾股定理即可求得
,再根据勾股定理即可求得![]() 的长 .
的长 .
(1)∵ △ABC是等腰直角三角形,∠ACB=90°,AC=![]() ,
,
∴![]() ,
, ![]() ,
,
过点C作![]() ,则
,则![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]()
![]() ,
,
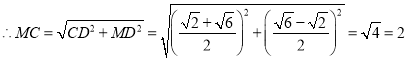 ,
,
![]() .
.
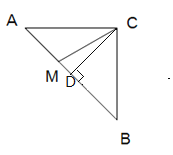
(2)过点C作CN⊥CM,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,
![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∵![]() ,
,
![]() ,
,
∵△ABC是等腰直角三角形,
∴CA=CB,∠ACB=90°
∴![]() ,
,
即![]()
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() .
.
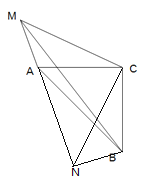
(3)过C作CD⊥CM且CD=CM,连接BD、MD,延长AM,DB交于E.
则![]() ,
,
∵△ABC是等腰直角三角形,
![]() ,
,
![]() ,
,
即![]() ,
,
![]()
![]()
又![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
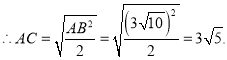

【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下,请补充完整.
收集数据 17 18 16 12 24 15 27 25 18 19
22 17 16 19 31 29 16 14 15 25
15 31 23 17 15 15 27 27 16 19
整理、描述数据
销售额/万元 | 12 | 14 | 15 | 16 | 17 | 18 | 19 | 22 | 23 | 24 | 25 | 27 | 29 | 31 |
人数 | 1 | 1 | 4 | 3 | 2 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
分析数据 样本数据的平均数、众数、中位数如下表所示:
平均数 | 众数 | 中位数 |
20 | 18 |
得出结论 ⑴如果想让一半左右的营业员都能达到销售目标,你认为月销售额应定为 万元.
⑵如果想确定一个较高的销售目标,这个目标可以定为每月 万元,理由为 .