题目内容
【题目】已知在半径为3的⊙O中,弦AB=3![]() ,弦AC=3,则∠BAC的度数为________.
,弦AC=3,则∠BAC的度数为________.
【答案】105° 或15°
【解析】
连接OA,过O作OE⊥AB,OF⊥AC,根据垂径定理求出AE,AF的值,根据解直角三角形的知识求出∠OAE=45°,∠OAF=60°,然后分情况求出∠BAC即可.
解:有两种情况:
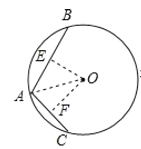
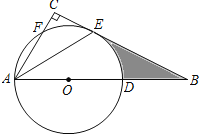
①如图,连接OA,过O作OE⊥AB,OF⊥AC
∴∠OEA=∠OFA=90°
由垂径定理得:AE=BE=![]() ,AF=CF=
,AF=CF=![]()
∴
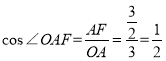
∴∠OAE=45°,∠OAF=60°
∴∠BAC=∠OAE+∠OAF=45°+60°=105°;
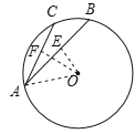
②如图,连接OA,过O作OE⊥AB,OF⊥AC
∴∠OEA=∠OFA=90°
由垂径定理得:AE=BE=![]() ,AF=CF=
,AF=CF=![]()
∴
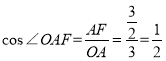
∴∠OAE=45°,∠OAF=60°
∴∠BAC=∠OAF-∠OAE=60°-45°=15°,
故答案为105°或15°.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣8 | ﹣3 | 0 | 1 | 0 | ﹣3 | … |
若A(m,y1),B(m﹣1,y2)两点都在该函数的图象上,当m满足范围_____时,y1<y2.