ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§
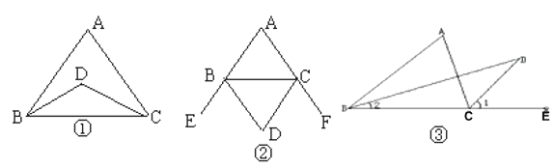
Θ®1Θ©»γΆΦΔΌΘ§BDΓΔCD «ΓœABCΚΆΓœACBΒΡΫ«ΤΫΖ÷œΏ«“œύΫΜ”ΎΒψDΘ§»τΓœA =70ΓψΘ§ ‘«σΓœBDCΒΡΕ» ΐΘ§≤ΔΥΒΟςάμ”…ΓΘ
Θ®2Θ©»γΆΦΔΎΘ§BDΓΔCDΖ÷±π «ΓςABCΆβΫ«ΓœEBCΓΔΓœFCBΒΡΤΫΖ÷œΏ«“œύΫΜ”ΎΒψDΘ§»τΓœA =xΓψΘ§ ‘”Οx±μ ΨΓœBDCΒΡΕ» ΐΘ§≤ΔΥΒΟςάμ”…ΓΘ
Θ®3Θ©»γΆΦΔέΘ§BDΓΔCDΖ÷±π «ΓœABCΚΆΓςACBΆβΫ«ΓœACEΒΡΤΫΖ÷œΏ«“œύΫΜ”ΎΒψDΘ§ ‘’“≥ωΓœA”κΓœBDC÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΓΘ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓœBDCΘΫ125ΓψΘ§άμ”…ΦϊΫβΈωΘΜΘ®2Θ©ΓœBDCΘΫ90Γψ![]() xΓψΘ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©ΓœBDCΘΫ
xΓψΘ§άμ”…ΦϊΫβΈωΘΜΘ®3Θ©ΓœBDCΘΫ![]() ΓœAΘ§άμ”…ΦϊΫβΈω.
ΓœAΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμ«σ≥ωΓœABCΘΪΓœACBΘΫ110ΓψΘ§‘ΌΗυΨίΫ«ΤΫΖ÷œΏΒΡ–‘÷ ΚΆ»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμ«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©œ»ΗυΨίΆβΫ«ΤΫΖ÷œΏΒΡ–‘÷ «σ≥ωΓœCBDΘΫ![]() Θ®ΓœAΘΪΓœACBΘ©Θ§ΓœBCDΘΫ
Θ®ΓœAΘΪΓœACBΘ©Θ§ΓœBCDΘΫ![]() Θ®ΓœAΘΪΓœABCΘ©Θ§‘Ό”…»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΫβ¥πΦ¥Ω…ΘΜ
Θ®ΓœAΘΪΓœABCΘ©Θ§‘Ό”…»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΫβ¥πΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨί»ΐΫ«–ΈΒΡ“ΜΗωΆβΫ«Β»”Ύ”κΥϋ≤ΜœύΝΎΒΡΝΫΗωΡΎΫ«ΒΡΚΆΩ…ΒΟΓœACEΘΫΓœAΘΪΓœABCΘ§ΓœDCEΘΫΓœDΘΪΓœDBCΘ§‘ΌΗυΨίΫ«ΤΫΖ÷œΏΒΡΕ®“εΩ…ΒΟΓœDBCΘΫ![]() ΓœABCΘ§ΓœDCEΘΫ
ΓœABCΘ§ΓœDCEΘΫ![]() ΓœACEΘ§»ΜΚσ’ϊάμΩ…ΒΟΓœBDCΘΫ
ΓœACEΘ§»ΜΚσ’ϊάμΩ…ΒΟΓœBDCΘΫ![]() ΓœA.
ΓœA.
ΫβΘΚΘ®1Θ©ΓœBDCΘΫ125ΓψΘ§
άμ”…ΘΚΓΏBDΓΔCD «ΓœABCΚΆΓœACBΒΡΫ«ΤΫΖ÷œΏΘ§
ΓύΓœDBCΘΫ![]() ΓœABCΘ§ΓœDCBΘΫ
ΓœABCΘ§ΓœDCBΘΫ![]() ΓœACBΘ§
ΓœACBΘ§
ΓΏΓœABCΘΪΓœACBΘΫ180ΓψΓœAΘΫ110ΓψΘ§
ΓύΓœBDCΘΫ180ΓψΓœDBCΓœDCBΘΫ180Γψ![]() Θ®ΓœABCΘΪΓœACBΘ©ΘΫ180Γψ55ΓψΘΫ125ΓψΘΜ
Θ®ΓœABCΘΪΓœACBΘ©ΘΫ180Γψ55ΓψΘΫ125ΓψΘΜ
Θ®2Θ©ΓœBDCΘΫ90Γψ![]() xΓψΘΜ
xΓψΘΜ
άμ”…ΘΚΓΏBDΓΔCDΖ÷±π «ΓςABCΆβΫ«ΓœEBCΓΔΓœFCBΒΡΤΫΖ÷œΏΘ§
ΓύΓœCBDΘΫ![]() Θ®ΓœAΘΪΓœACBΘ©Θ§ΓœBCDΘΫ
Θ®ΓœAΘΪΓœACBΘ©Θ§ΓœBCDΘΫ![]() Θ®ΓœAΘΪΓœABCΘ©Θ§
Θ®ΓœAΘΪΓœABCΘ©Θ§
ΓΏΓœABCΘΪΓœACBΘΫ180ΓψΓœAΘ§
ΓύΓœBDCΘΫ180ΓψΓœCBDΓœBCD
ΘΫ180Γψ![]() Θ®ΓœAΘΪΓœACBΘΪΓœAΘΪΓœABCΘ©
Θ®ΓœAΘΪΓœACBΘΪΓœAΘΪΓœABCΘ©
ΘΫ180Γψ![]() Θ®2ΓœAΘΪ180ΓψΓœAΘ©
Θ®2ΓœAΘΪ180ΓψΓœAΘ©
ΘΫ90Γψ![]() ΓœAΘ§
ΓœAΘ§
Φ¥ΓœBDCΘΫ90Γψ![]() xΓψΘΜ
xΓψΘΜ
Θ®3Θ©ΓœBDCΘΫ![]() ΓœAΘ§
ΓœAΘ§
άμ”…ΘΚ”…»ΐΫ«–ΈΒΡΆβΫ«–‘÷ Ω…ΒΟΘ§ΓœACEΘΫΓœAΘΪΓœABCΘ§ΓœDCEΘΫΓœDΘΪΓœDBCΘ§
ΓΏBDΓΔCDΖ÷±π «ΓœABCΚΆΓςACBΆβΫ«ΓœACEΒΡΤΫΖ÷œΏΘ§
ΓύΓœDBCΘΫ![]() ΓœABCΘ§ΓœDCEΘΫ
ΓœABCΘ§ΓœDCEΘΫ![]() ΓœACEΘ§
ΓœACEΘ§
Γύ![]() Θ®ΓœAΘΪΓœABCΘ©ΘΫΓœDΘΪ
Θ®ΓœAΘΪΓœABCΘ©ΘΫΓœDΘΪ![]() ΓœABCΘ§
ΓœABCΘ§
ΓύΓœBDCΘΫ![]() ΓœA.
ΓœA.