题目内容
【题目】如图,已知直角坐标平面内的两点A(3,2),点B (6,0)过点B作Y轴的平行线交直线OA于点C
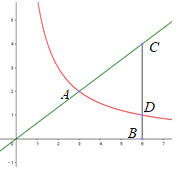
(1)求直线OA所对应的函数解析式
(2)若某一个反比例函数的图像经过点A,且交BC于点D,联结AD,求△ACD的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设直线OA的解析式为y=kx(k≠0),把A点坐标代入解析式,求出k的值即可;
(2)过A作AE⊥x轴于点E,连接AD,根据S△ACD=S△CBO-S△AEO-S梯形ADBE求解即可.
(1)设直线OA的解析式为y=kx(k≠0),
∵A(3,2)在直线OA上,
∴2=3k
解得,k=![]() ,
,
∴直线OA的解析式为![]() ;
;
(2)过A作AE⊥x轴于点E,连接AD,如图所示,
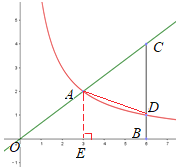
∵A(3,2)
∴OE=3,AE=2,
设反比例函数解析式为:![]() ,
,
∵A(3,2)
∴k=2×3=6
∴![]() ,
,
∵B(6,0)
∴D(6,1),C(6,4)
∴OB=6,BE=OB-OE=3,BD=1,BC=4,
∴S△ACD=S△CBO-S△AEO-S梯形ADBE
=![]()
=![]()
=![]() .
.

练习册系列答案
相关题目