ЬтФПФкШн
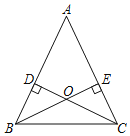
ЁОЬтФПЁПШчЭМ1ЃЌдкЕШбќжБНЧШ§НЧаЮABCжаЃЌЁЯACBЃН90ЁуЃЌBCЃНmЃЌНЋБпABШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮBDЃЌЙ§ЕуDзїDEЁЭCBНЛCBЕФбгГЄЯпгкЕуEЃЌСЌНгCDЃЎ
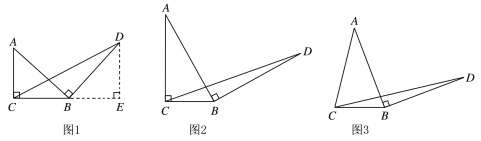
ЃЈ1ЃЉжБНгаДГіЁїBCDЕФУцЛ§ЮЊЁЁ ЁЁЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌдквЛАуЕФRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌBCЃНmЃЌНЋБпABШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮBDЃЌСЌНгCDЃЌгУКЌmЕФЪНзгБэЪОЁїBCDЕФУцЛ§ЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌдкЕШбќЁїABCжаЃЌABЃНACЃЌBCЃН8ЃЌНЋБпABШЦЕуBЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮBDЃЌСЌНгCDЃЌдђЁїBCDЕФУцЛ§ЮЊЁЁ ЁЁЃЛШєBCЃНmЃЌдђЁїBCDЕФУцЛ§ЮЊЁЁ ЁЁЃЈгУКЌmЕФЪНзгБэЪОЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУAASжЄУї![]() ЃЌПЩЧѓГіЁїBCDЕФЕзКЭИпЃЌНјЖјПЩЧѓЦфУцЛ§ЃЛЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЬэМгИЈжњЯпЕФЗНЗЈЃЌзї
ЃЌПЩЧѓГіЁїBCDЕФЕзКЭИпЃЌНјЖјПЩЧѓЦфУцЛ§ЃЛЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЬэМгИЈжњЯпЕФЗНЗЈЃЌзї![]() НЛCBЕФбгГЄЯпгкЕуGЃЌгЩжБНЧШ§НЧаЮНЧжЎМфЕФЙиЯЕПЩЕУ
НЛCBЕФбгГЄЯпгкЕуGЃЌгЩжБНЧШ§НЧаЮНЧжЎМфЕФЙиЯЕПЩЕУ![]() ЃЌРћгУAASвзжЄ
ЃЌРћгУAASвзжЄ![]() ЃЌПЩЕУDGГЄЃЌНјЖјПЩЧѓУцЛ§ЃЛ
ЃЌПЩЕУDGГЄЃЌНјЖјПЩЧѓУцЛ§ЃЛ
ЃЈ3ЃЉзїANЁЭBCНЛBCгкЕуNЃЌзї![]() НЛCBЕФбгГЄЯпгкЕуMЃЌгЩЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪПЩжЊ
НЛCBЕФбгГЄЯпгкЕуMЃЌгЩЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪПЩжЊ![]() ЃЌРћгУЃЈ2ЃЉжаЫМТЗжЄУї
ЃЌРћгУЃЈ2ЃЉжаЫМТЗжЄУї![]() ЃЌПЩЕУDMГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНЧѓУцЛ§МДПЩ.
ЃЌПЩЕУDMГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНЧѓУцЛ§МДПЩ.
НтЃКЃЈ1ЃЉ![]() ЪЧЕШбќжБНЧШ§НЧаЮ
ЪЧЕШбќжБНЧШ§НЧаЮ
![]()
гЩа§зЊЕФаджЪПЩжЊ![]()
![]()
![]()
![]()
дк![]() КЭ
КЭ![]() жа
жа
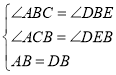
![]()
![]()
![]()
ЃЈ2ЃЉзї![]() НЛCBЕФбгГЄЯпгкЕуG
НЛCBЕФбгГЄЯпгкЕуG
![]()
![]()
гЩа§зЊЕУAB=DB
дк![]() КЭ
КЭ![]() жа
жа
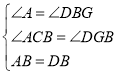
![]()
![]()
![]()
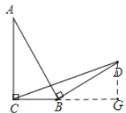
ЃЈ3ЃЉзїANЁЭBCНЛBCгкЕуNЃЌзї![]() НЛCBЕФбгГЄЯпгкЕуM
НЛCBЕФбгГЄЯпгкЕуM
![]()
![]()
![]()
![]()
![]()
гЩа§зЊЕУAB=DB
дк![]() КЭ
КЭ![]() жа
жа
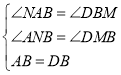
![]()
![]()
![]()
ШєBCЃНmЃЌдђ![]()
![]()

 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ
ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ