题目内容
一段公路的坡度为1︰3，某人沿这段公路路面前进100米，那么他上升的最大高度是
| A．30米 | B．10米 | C． 米 | D． 米 |
D
分析：已知了坡面长为100米，可根据坡度比设出两条直角边的长度，根据勾股定理可列方程求出坡面的铅直高度，即此人上升的最大高度．
解：如图．
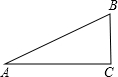
Rt△ABC中，tanA=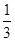
，AB=100米．
设BC=x米，则AC=3x米，根据勾股定理，得：
x2+（3x）2=1002，
解得x=（负值舍去）．
故选D．
解：如图．
Rt△ABC中，tanA=
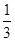，AB=100米．设BC=x米，则AC=3x米，根据勾股定理，得：
x2+（3x）2=1002，
解得x=
（负值舍去）．故选D．
练习册系列答案
阅读快车系列答案
相关题目
的坡面向上走50米，则此人离地面的高度为( )
ABC中，∠B = 45°，∠C = 60°，AB = 6。求BC的长（结果保留根号）。
上建有一座电信信号发射架
，现在山脚
处测得峰顶的仰角为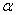
，发射架顶端的仰角为
，其中
，求发射架高
的斜坡上，斜坡上的平面镜反射成与地面平行的光线，则这束光线与坡面的夹角
是 度.
x=2sin45°-1