题目内容
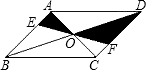
如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，若平行四边形的面积是12，则△AOE与△DOF的面积和为
- A.4
- B.3
- C.2
- D.6
B
分析：根据平行四边形的性质可知△AOE≌△OCF，则求△AOE与△DOF的面积和转化为求△DOC的面积．
解答：∵平行四边形ABCD，
∴OA=OC，∠OAE=∠OCF，∠OFC=∠OEA，
∴△AOE≌△OCF，
∴S阴=S△DOF+S△COF=S△DOC=
S?ABCD=
=3，
故选B．
点评：本题考查了平行四边形的性质，根据平行四边形的性质，结合全等三角形求解．
分析：根据平行四边形的性质可知△AOE≌△OCF，则求△AOE与△DOF的面积和转化为求△DOC的面积．
解答：∵平行四边形ABCD，
∴OA=OC，∠OAE=∠OCF，∠OFC=∠OEA，
∴△AOE≌△OCF，
∴S阴=S△DOF+S△COF=S△DOC=
S?ABCD==3，故选B．
点评：本题考查了平行四边形的性质，根据平行四边形的性质，结合全等三角形求解．
练习册系列答案
相关题目
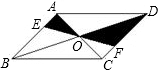如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，那么阴影部分的面积是平行四边形ABCD面积的（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
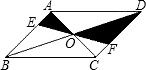如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，若平行四边形的面积是12，则△AOE与△DOF的面积和为（ ）
如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，那么阴影部分的面积是平行四边形ABCD面积的
