题目内容
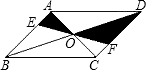
如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，那么阴影部分的面积是平行四边形ABCD面积的
- A.
- B.
- C.
- D.
B
分析：由平行四边形的性质得到OA=OC，OB=OD，AB∥DC，证出△AOE和△COF全等，△AOB和△COD全等，得到面积相等，即可得到选项．
解答：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，AB∥DC，
∴△AOE≌△COF，
∴S△AOE=S△COF，
∵∠AOD=∠COB，
∴△COB≌△AOD，
∴S△AOD=S△BOC，
同理S△AOB=S△DOC
∵0B=0D，
∴S△AOB=S△DOC，
∴阴影部分的面积是S△AOE+S△DOF=S△DOC=S平行四边形ABCD．
故选B．
点评：本题主要考查了平行四边形的性质和判定，全等三角形的性质和判定等知识点，解此题的关键是证明两个三角形全等．
分析：由平行四边形的性质得到OA=OC，OB=OD，AB∥DC，证出△AOE和△COF全等，△AOB和△COD全等，得到面积相等，即可得到选项．
解答：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，AB∥DC，
∴△AOE≌△COF，
∴S△AOE=S△COF，
∵∠AOD=∠COB，
∴△COB≌△AOD，
∴S△AOD=S△BOC，
同理S△AOB=S△DOC
∵0B=0D，
∴S△AOB=S△DOC，
∴阴影部分的面积是S△AOE+S△DOF=S△DOC=
S平行四边形ABCD．故选B．
点评：本题主要考查了平行四边形的性质和判定，全等三角形的性质和判定等知识点，解此题的关键是证明两个三角形全等．
练习册系列答案
金钥匙试卷系列答案
相关题目
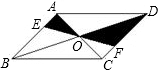如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，那么阴影部分的面积是平行四边形ABCD面积的（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
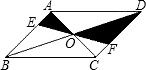如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，若平行四边形的面积是12，则△AOE与△DOF的面积和为（ ）
如图，直线EF过平行四边形ABCD对角线的交点O，分别交AB、CD于E、F，若平行四边形的面积是12，则△AOE与△DOF的面积和为