题目内容
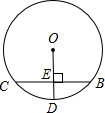
如图，⊙O的直径CD垂直于弦AB，垂足为点P，若AP=6cm，PD=4cm，则⊙O的直径为______cm．
如图，连接OA．
∵OA=OD（⊙O的半径），OP+PD=OD，PD=4cm，
∴OP=OA-4cm；
∵⊙O的直径CD垂直于弦AB，
∴∠APO=90°，
∴OA2=AP2+OP2，即OA2=（6cm）2+（OA-4cm）2，
∴OA=
cm，
∴⊙O的直径为：2OA=13cm．
故答案是：13．
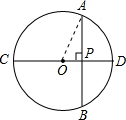
∵OA=OD（⊙O的半径），OP+PD=OD，PD=4cm，
∴OP=OA-4cm；
∵⊙O的直径CD垂直于弦AB，
∴∠APO=90°，
∴OA2=AP2+OP2，即OA2=（6cm）2+（OA-4cm）2，
∴OA=
| 13 |
| 2 |
∴⊙O的直径为：2OA=13cm．
故答案是：13．
练习册系列答案
阅读快车系列答案
相关题目
