题目内容
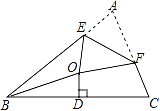
【题目】如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.
(1)求BE的长;
(2)判断△BDE的形状,并说明理由. 
【答案】(1)9;(2)△BDE为等腰三角形.理由见解析.
【解析】试题分析:(1)根据等边三角形的性质得BC=AB=6cm,再根据“三线合一”得AD=CD=![]() AC=3cm,而CD=CE=3cm,所以BE=BC+CE=9cm;
AC=3cm,而CD=CE=3cm,所以BE=BC+CE=9cm;
(2)根据等边三角形的性质得∠ABC=∠ACB=60°,再根据“三线合一”得∠CBD=![]() ∠ABC=30°,而CD=CE,则∠CDE=∠E,接着利用三角形外角性质得∠CDE+∠E=∠ACB=60°,所以∠E=30°,于是得到∠CBD=∠E,然后根据等腰三角形的判定即可得到△BDE为等腰三角形.
∠ABC=30°,而CD=CE,则∠CDE=∠E,接着利用三角形外角性质得∠CDE+∠E=∠ACB=60°,所以∠E=30°,于是得到∠CBD=∠E,然后根据等腰三角形的判定即可得到△BDE为等腰三角形.
试题解析:
(1)∵△ABC为等边三角形,
∴BC=AB=6cm,
∵BD⊥AC,
∴AD=CD=![]() AC=3cm,
AC=3cm,
∵CD=CE=3cm,
∴BE=BC+CE=6cm+3cm=9cm; ..........3分
(2)△BDE为等腰三角形.理由如下:
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵BD⊥AC,
∴∠CBD=![]() ∠ABC=30°,
∠ABC=30°,
∵CD=CE,
∴∠CDE=∠E,
而∠CDE+∠E=∠ACB=60°,
∴∠E=30°,
∴∠CBD=∠E,
∴△BDE为等腰三角形

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目