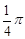题目内容
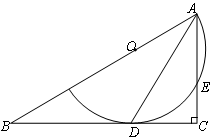
如图,Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 等于
等于

 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 等于
等于
| A.4 | B.3.5 | C.3 | D.2.5 |
C
分析:如图,过点E作EF⊥BC于点,
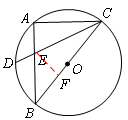
∵Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,∴AB=5。
∵D是
 的中点,∴∠ACD=∠DCE。∴AE=EF。
的中点,∴∠ACD=∠DCE。∴AE=EF。设AE="EF=" x,则BE=
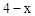 。
。由△BCE的面积公式,得
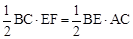 ,即
,即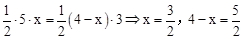 。∴AE=
。∴AE=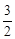 ,BE=
,BE=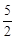 。
。在Rt△ACE中,由勾股定理得,
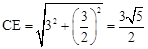 。
。由相交弦定理,得
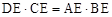 ,即
,即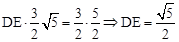 。
。∴
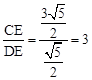 。故选C。
。故选C。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在△ABC中,∠ABC=90°,边AC的垂直平分线交BC于点D,交AC于点E,连接BE.

(1)若∠C=30°,求证:BE是△DEC外接圆的切线;
(2)若BE= ,BD=1,求△DEC外接圆的直径.
,BD=1,求△DEC外接圆的直径.

(1)若∠C=30°,求证:BE是△DEC外接圆的切线;
(2)若BE=
 ,BD=1,求△DEC外接圆的直径.
,BD=1,求△DEC外接圆的直径.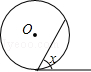









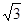 ,求圆弧的半径.
,求圆弧的半径.