��Ŀ����
����Ŀ���������ı����߶���ȣ��ĸ��Ƕ���90�㣮��ͼ����֪������ABCD��ֱ��MN���Ϸ���BC��ֱ��MN�ϣ���E��ֱ��MN��һ�㣬��AEΪ����ֱ��MN���Ϸ���������AEFG�� 
��1����ͼ1������E���߶�BC�ϣ������B��C�غϣ�ʱ�� 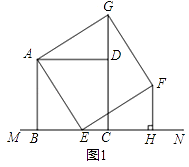
���жϡ�ADG���ABE�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڹ���F��FH��MN������Ϊ��H���۲첢�²��߶�BE���߶�CH��������ϵ����˵�����ɣ�
��2����ͼ2������E������CN�ϣ������C�غϣ�ʱ�� 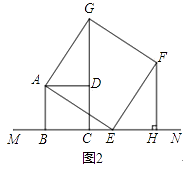
���жϡ�ADG���ABE�Ƿ�ȫ�ȣ�����˵�����ɣ�
�ڹ���F��FH��MN������Ϊ��H����֪GD=4�����CFH�������
���𰸡�
��1���⣺�١�BAE�ա�DAG���������£�
���ı���ABCD���ı���AEFG�������Σ�
��AB=AD��AE=AG����BAD=��EAG=90�㣬
���BAE+��EAD=��DAG+��EAD��
���BAE=��DAG��
���BAE�ա�DAG��
��CH=BE���������£�
����֪�ɵá�EAG=��BAD=��AEF=90�㣬
�ɢٵá�FEH=��BAE=��DAG��
�֡�G������CD�ϣ�
��GDA=��EHF=��EBA=90�㣬AG=AE=EF��
���BAE=��DAG=��EFH��
���EFH�ա�GAD����EFH�ա�ABE��
��EH=AD=BC��
��CH=BE��
��2���⣺�١�BAE�ա�DAG���������£�
���ı���ABCD���ı���AEFG�������Σ�
��AB=AD��AE=AG����ADG=��ABE=90�㣬
����Rt��BAE��Rt��DAG��
���BAE�ա�DAG����HL��
���ɣ�1��ͬ���ɵã���EFH�ա�AGD����EFH�ա�AEB��
��GD=FH=CH=4��
���CFH������� ![]() FHCH=
FHCH= ![]() ��4��4=8
��4��4=8
����������1�������������ε����ʼ�SAS���������ADG�ա�ABE��������ȫ�������ε����ʼ��ɽ�𣻢����������ε����ʼ�SAS���������ADG�ա�ABE��������ȫ�������ε����ʼ��ɽ�𣻣�2��������HL����֤����BAE�ա�DAG���ɣ������á�EFH�ա�GAD����EFH�ա�ABE�����ɵó�GD=FH=CH=4�������á�CFH�������ʽ�����