题目内容
【题目】如图，点O是直线AB上一点，∠AOE＝130°，∠EOF＝90°，OP平分∠AOE，OQ平分∠BOF，求∠POQ的度数．
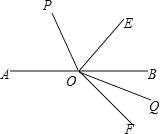
【答案】∠POQ＝135°．
【解析】
依据角平分线的定义即可得到∠POE的度数，再根据邻补角的定义即可得到∠BOE的度数，进而得出∠BOF 的度数，再根据角平分线的定义，即可得到∠BOQ的度数，最后依据∠POQ＝∠POE+∠BOE+∠BOQ进行计算即可．
解：∵OP平分∠AOE，
∴∠POE＝
∠AOE＝×130°＝65°，
∵∠BOE＝180°﹣∠AOE＝180°﹣130°＝50°，
∴∠BOF＝∠EOF﹣∠BOE＝90°﹣50°＝40°，
∵OQ平分∠BOF，
∴∠BOQ＝∠BOF＝×40°＝20°，
∴∠POQ＝∠POE+∠BOE+∠BOQ＝65°+50°+20°＝135°．
练习册系列答案
相关题目
【题目】某公司有
、
两种型号的客车共20辆，它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下，共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求、两种型号的客车各有多少辆?
(2)某中学计划租用、两种型号的客车共8辆，同时送七年级师生到沙家浜参加社会实践活动，已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车？
