题目内容
【题目】如图，点D是BC的中点，DE垂直平分AC，垂足为E，F是BA的中点．求证：DF是AB的垂直平分线．
【答案】连接AD．
【解析】
试题本题考查了线段的垂直平分线的判定和性质，全等三角形的判定和性质，垂直的定义，熟练掌握线段的垂直平分线的性质是解题的关键．连接AD，根据垂直平分线的性质得到AD=DC，由BD=CD，等量代换得到AD=BD，推出△ADF≌△BDF，根据全等三角形的性质得到∠AFD=∠BFD，然后根据平角的定义即可得到结论．
试题解析：证明：连接AD，
∵DE垂直平分AC，
∴AD=DC，
∵点D是BC的中点，
∴BD=CD，
∴AD=BD，
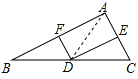
在△ADF与△BDF中，
，
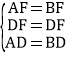∴△ADF≌△BDF，
∴∠AFD=∠BFD，
∵∠AFD+∠BFD=180°，
∴∠AFD=∠BFD=90°，
∴DF⊥AB，
∴DF是AB的垂直平分线．
练习册系列答案
英才计划期末调研系列答案
相关题目
【题目】有这样一个问题：探究函数y= 
的图象与性质． 下面是小文的探究过程，请补充完整：
（1）函数y= 的自变量x的取值范围是；
（2）如表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | 0 | 2 | | | | … |
如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．
①观察图中各点的位置发现：点A1和B1 ， A2和B2 ， A3和B3 ， A4和B4均关于某点中心对称，则该点的坐标为；
②小文分析函数y= 的表达式发现：当x＜1时，该函数的最大值为0，则该函数图象在直线x=1左侧的最高点的坐标为；
（3）小文补充了该函数图象上两个点（ 
，﹣ 
），（ 
， 
）， ①在上图中描出这两个点，并画出该函数的图象；
②写出该函数的一条性质： ．
