题目内容
如图，已知点A（-4，0），B（1，0），∠C=90°，AC=| 5 |
（1）求∠CAB的正弦、余弦和正切值；（2）点C的坐标．
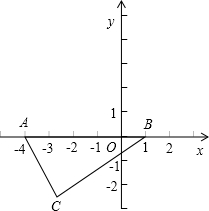
分析：（1）已知两边，利用勾股定理求出另一边，解直角三角形即可．
（2）纵坐标等于-ACsinA，横坐标等于1-BCcosB．
（2）纵坐标等于-ACsinA，横坐标等于1-BCcosB．
解答：解：（1）BC=
=2
；
sinA=
tanA=2；
cosA=
．
（2）-ACsinA=-2，1-BCcosB=-3
故点C的坐标（-3，-2）．
| AB2 - AC2 |
| 5 |
sinA=
| 2 |
| 5 |
| 5 |
tanA=2；
cosA=
| ||
| 5 |
（2）-ACsinA=-2，1-BCcosB=-3
故点C的坐标（-3，-2）．
点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．
练习册系列答案
相关题目
16、如图，已知点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足分别为A，C、下列结论错误的是（ ）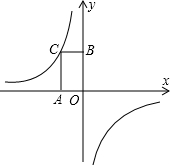
如图，已知点C为反比例函数y=-
如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10cm．图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设
如图，已知点C为AB上一点，AC=12cm，CB=