题目内容
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
分析:由AD∥BC,AC平分∠BCD,∠ADC=120°,得到∠1=∠2=∠3=30°,∠B=60°,于是有AB=AD=DC,且∠BAC=90°,得到BC为直径,设圆心为O,AB=x,则BC=2AB=2x,∠4=2∠1=60°,然后利用四边形ABCD的周长为10cm,可求出半径;而S阴影部分=S扇形OAD-S△OAD,利用扇形的面积公式:S=
和等边三角形的面积分别计算它们的面积即可.
| nπR2 |
| 360 |
解答: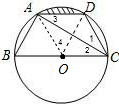 解:如图,
解:如图,
∵AC平分∠BCD,
∴∠1=∠2,
又∵AD∥BC,
∴∠1=∠2=∠3,
而∠ADC=120°,
∴∠1=∠2=∠3=30°,∠B=60°,
∴AB=AD=DC,且∠BAC=90°,
∴BC为直径,设圆心为O,AB=x,则BC=2AB=2x,∠4=2∠1=60°,
又∵四边形ABCD的周长为10cm,
∴x+x+x+2x=10,解得x=2,即⊙O的半径为2,
连OA,OD,
∴S阴影部分=S扇形OAD-S△OAD=
-
×22=
-
.
故选B.
 解:如图,
解:如图,∵AC平分∠BCD,
∴∠1=∠2,
又∵AD∥BC,
∴∠1=∠2=∠3,
而∠ADC=120°,
∴∠1=∠2=∠3=30°,∠B=60°,
∴AB=AD=DC,且∠BAC=90°,
∴BC为直径,设圆心为O,AB=x,则BC=2AB=2x,∠4=2∠1=60°,
又∵四边形ABCD的周长为10cm,
∴x+x+x+2x=10,解得x=2,即⊙O的半径为2,
连OA,OD,
∴S阴影部分=S扇形OAD-S△OAD=
| 60π×4 |
| 360 |
| ||
| 4 |
| 2π |
| 3 |
| 3 |
故选B.
点评:本题考查了扇形的面积公式:S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S=
lR,l为扇形的弧长,R为半径.同时考查了圆周角定理及其推论以及等边三角形的面积.
| nπR2 |
| 360 |
| 1 |
| 2 |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )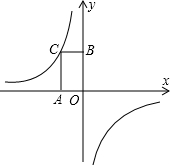 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=