题目内容
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设| BA |
| a |
| BC |
| b |
（1）在图中画出向量
| BD |
| a |
| b |
（2）试用
| a |
| b |
| BD |
分析：（1）首先过点D作DE∥BC，交AB于E，作DF∥AB，交BC于F，利用平行四边形法则，即可得DF向量
在
方向上的分向量为
，向量
在
方向上的分向量为
；
（2）由AD：DC=3；4，可得
=
，又由
=
+
，即可求得答案．
| BD |
| a |
| BE |
| BD |
| b |
| BF |
（2）由AD：DC=3；4，可得
| AD |
| 3 |
| 7 |
| AC |
| BD |
| BA |
| AD |
解答：
解：（1）如图，过点D作DE∥BC，交AB于E，作DF∥AB，交BC于F，
则DF向量
在
方向上的分向量为
，
向量
在
方向上的分向量为
；
（2）∵AD：DC=3：4，
∴AD：AC=3：7，
∴
=
，
∴
=
+
=
+
=
+
（
+
）=
+
（-
+
）=
+
．
解：（1）如图，过点D作DE∥BC，交AB于E，作DF∥AB，交BC于F，则DF向量
| BD |
| a |
| BE |
向量
| BD |
| b |
| BF |
（2）∵AD：DC=3：4，
∴AD：AC=3：7，
∴
| AD |
| 3 |
| 7 |
| AC |
∴
| BD |
| BA |
| AD |
| BA |
| 3 |
| 7 |
| AC |
| BA |
| 3 |
| 7 |
| AB |
| BC |
| a |
| 3 |
| 7 |
| a |
| b |
| 4 |
| 7 |
| a |
| 3 |
| 7 |
| b |
点评：此题考查了平面向量的知识．此题难度适中，注意掌握平行四边形法则与三角形法则是解此题的关键，注意数形结合思想的应用．
练习册系列答案
相关题目
如图，已知点C为线段AE上一点，AE=8cm，△ABC和△CDE为AE同侧的两个等边三角形，连接BE交CD于N，连接AD交BC于M，连接MN．
（2012•龙湖区模拟）如图，已知点P为反比例函数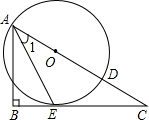
（2012•玉林）如图，已知点O为Rt△ABC斜边AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D，连接AE．
如图，已知点D为等腰直角△ABC内一点，AC=BC，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．若DE=acm，BD=bcm（a＞b），则CD=