题目内容
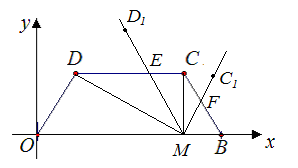
如图,在平面直角坐标系中,O为坐标原点为,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.

(1)求直线CB的解析式;
(2)求点M的坐标;
(3)∠DMC绕点M顺时针旋转α (30°<α<60°)后,得到∠D1MC1(点D1,C1依次与点D,C对应),射线MD1交直线DC于点E,射线MC1交直线CB于点F ,设DE=m,BF=n .求m与 n的函数关系式.

(1)求直线CB的解析式;
(2)求点M的坐标;
(3)∠DMC绕点M顺时针旋转α (30°<α<60°)后,得到∠D1MC1(点D1,C1依次与点D,C对应),射线MD1交直线DC于点E,射线MC1交直线CB于点F ,设DE=m,BF=n .求m与 n的函数关系式.
(1)y=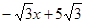 (2) M (1,0)或(4,0) (3)m=
(2) M (1,0)或(4,0) (3)m=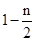
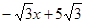 (2) M (1,0)或(4,0) (3)m=
(2) M (1,0)或(4,0) (3)m=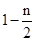
(1)BC解析式:y=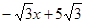 (2) 略证:△ODM∽△BMC
(2) 略证:△ODM∽△BMC 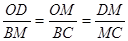 设OM=x,2×2=x(5-x), x=1或4, M (1,0)或(4,0)
设OM=x,2×2=x(5-x), x=1或4, M (1,0)或(4,0)
(3)当M (1,0)时,△DME∽△CMF,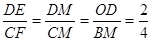
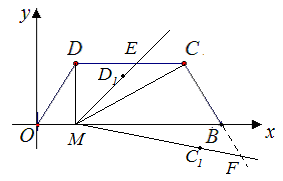
CF=2+n,DE=m,∴2+n=2m,即m=1+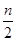
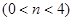
当M(4 ,0) 时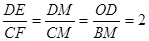 ∴m=2(2-n),即m=4-2n
∴m=2(2-n),即m=4-2n 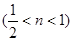
(1)由已知求得C点坐标,根据待定系数法求得直线CB的解析式
(2)先证明△ODM∽△BMC.得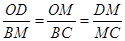 ,所以OD•BC=BM•OM.设OM=x,则BM=5-x,得2×2=x(5-x),解得x的值,即可求得M点坐标;
,所以OD•BC=BM•OM.设OM=x,则BM=5-x,得2×2=x(5-x),解得x的值,即可求得M点坐标;
(3)(Ⅰ)当M点坐标为(1,0)时,如图2,OM=1,BM=4.先求得DME∽△CMF,所以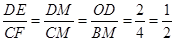 ,可得CF=2DE.所以2-n=2m,即m=
,可得CF=2DE.所以2-n=2m,即m=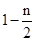 .(Ⅱ)当M点坐标为(4,0)时,OM=4,由OM<3,得出不合题意,舍去.
.(Ⅱ)当M点坐标为(4,0)时,OM=4,由OM<3,得出不合题意,舍去.
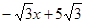 (2) 略证:△ODM∽△BMC
(2) 略证:△ODM∽△BMC 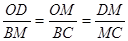 设OM=x,2×2=x(5-x), x=1或4, M (1,0)或(4,0)
设OM=x,2×2=x(5-x), x=1或4, M (1,0)或(4,0) (3)当M (1,0)时,△DME∽△CMF,
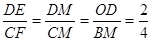
CF=2+n,DE=m,∴2+n=2m,即m=1+
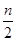
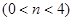

当M(4 ,0) 时
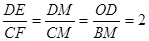 ∴m=2(2-n),即m=4-2n
∴m=2(2-n),即m=4-2n 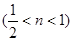

(1)由已知求得C点坐标,根据待定系数法求得直线CB的解析式
(2)先证明△ODM∽△BMC.得
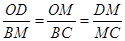 ,所以OD•BC=BM•OM.设OM=x,则BM=5-x,得2×2=x(5-x),解得x的值,即可求得M点坐标;
,所以OD•BC=BM•OM.设OM=x,则BM=5-x,得2×2=x(5-x),解得x的值,即可求得M点坐标;(3)(Ⅰ)当M点坐标为(1,0)时,如图2,OM=1,BM=4.先求得DME∽△CMF,所以
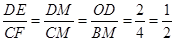 ,可得CF=2DE.所以2-n=2m,即m=
,可得CF=2DE.所以2-n=2m,即m=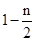 .(Ⅱ)当M点坐标为(4,0)时,OM=4,由OM<3,得出不合题意,舍去.
.(Ⅱ)当M点坐标为(4,0)时,OM=4,由OM<3,得出不合题意,舍去.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

 地的沙尘暴一直向正南方向移动,其移动速度
地的沙尘暴一直向正南方向移动,其移动速度 (km/h)与时间
(km/h)与时间 (h)的函数图象如图所示.过线段
(h)的函数图象如图所示.过线段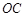 上一点
上一点 作横轴的垂线
作横轴的垂线 ,梯形
,梯形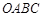 在直线
在直线 (km).
(km).
 时,求
时,求 城位于
城位于
 得到直线
得到直线 ,就要把直线
,就要把直线 个单位
个单位 ,且
,且 ,则函数
,则函数 与
与 在同一坐标系中的图象不可能是 ( )
在同一坐标系中的图象不可能是 ( )
 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料 ,一套
,一套 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料 ,工厂现有库存木料
,工厂现有库存木料 .
. (元)与生产
(元)与生产 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用 生产成本
生产成本 运费)
运费)


 与直线
与直线 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于 的不等式
的不等式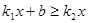 的解为___________。
的解为___________。