题目内容
A、B两地的路程为16千米,往返于两地的公交车单程运行40分钟.某日甲车比乙车早20分钟从A地出发,到达B地后立即返回,乙车出发20分钟后因故停车10分钟,随后按原速继续行驶,并与返回途中的甲车相遇.图13是乙车距A地的路程y (千米)与所用时间x (分)的函数图象的一部分(假设两车都匀速行驶).

⑴请在图13中画出甲车在这次往返中,距A地的路程y (千米)与时间x (分)的函数图象;
⑵乙车出发多长时间两车相遇?

⑴请在图13中画出甲车在这次往返中,距A地的路程y (千米)与时间x (分)的函数图象;
⑵乙车出发多长时间两车相遇?
解:(1)画出点P、M、N;
(2)方法1.
设直线EF的解析式为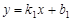 .
.
根据题意知,E(30,8),F(50,16),
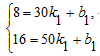
解得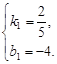 ∴
∴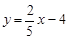 .①
.①
设直线MN的解析式为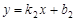 .
.
根据题意知,M(20,16),N(60,0),
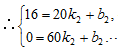
解得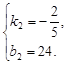 ∴
∴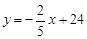 .②
.②
由①、②得方程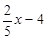
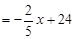 ,解得
,解得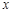 =35.
=35.
答:乙车出发35分钟两车相遇.
方法2.
公交车的速度为16÷40=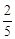 (千米/分).
(千米/分).
设乙车出发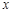 分钟两车相遇.
分钟两车相遇.
根据题意,得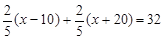 ,
,
解得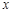 =35.
=35.
答:乙车出发35分钟两车相遇.
方法3.
公交车的速度为16÷40=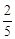 (千米/分).
(千米/分).
设乙车出发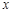 分钟两车相遇.
分钟两车相遇.
根据题意,得 ,
,
解得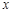 =35.
=35.
答:乙车出发35分钟两车相遇.
方法4.由题意知:M(20,16),F(50,16),C(10,0),
∵△DMF∽△DNC,∴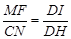
∴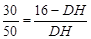 ,∴DH=10;
,∴DH=10;
∵△CDH∽△CFG,∴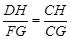 ,∴
,∴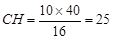 ;
;
∴OH=OC+CH=10+25=35.
答:乙车出发35分钟两车相遇.
(2)方法1.
设直线EF的解析式为
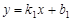 .
.根据题意知,E(30,8),F(50,16),
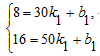
解得
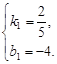 ∴
∴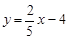 .①
.①设直线MN的解析式为
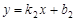 .
.根据题意知,M(20,16),N(60,0),
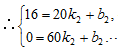
解得
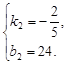 ∴
∴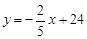 .②
.②由①、②得方程
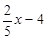
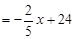 ,解得
,解得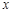 =35.
=35. 答:乙车出发35分钟两车相遇.
方法2.
公交车的速度为16÷40=
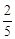 (千米/分).
(千米/分).设乙车出发
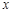 分钟两车相遇.
分钟两车相遇.根据题意,得
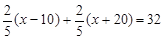 ,
,解得
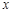 =35.
=35.答:乙车出发35分钟两车相遇.
方法3.
公交车的速度为16÷40=
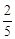 (千米/分).
(千米/分). 设乙车出发
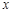 分钟两车相遇.
分钟两车相遇.根据题意,得
 ,
,解得
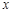 =35.
=35. 答:乙车出发35分钟两车相遇.
方法4.由题意知:M(20,16),F(50,16),C(10,0),
∵△DMF∽△DNC,∴
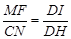
∴
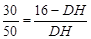 ,∴DH=10;
,∴DH=10;∵△CDH∽△CFG,∴
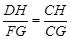 ,∴
,∴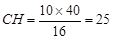 ;
;∴OH=OC+CH=10+25=35.
答:乙车出发35分钟两车相遇.
(1)根据甲、乙运动的速度与时间特征即可作出图象;
(2)可根据一次函数交点坐标的特征求得结果,也可根据行程问题设出未知数,列方程求解,亦可根据相似三角形的性质计算。
(2)可根据一次函数交点坐标的特征求得结果,也可根据行程问题设出未知数,列方程求解,亦可根据相似三角形的性质计算。

练习册系列答案
相关题目
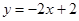 向右平移2个单位后的直线的解析式为 。
向右平移2个单位后的直线的解析式为 。

 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度 水流速度.】
水流速度.】 的距离是 。
的距离是 。

