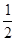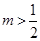题目内容
某家庭装修房屋,先由甲装修公司单独装修3天,剩下的工作由甲、乙两个装修公司合作完成.工程进度满足如图所示的函数关系,该家庭共支付工资8000元.
(1)求合作部分工作量y与工作时间x之间的函数关系式;
(2)完成此房屋装修共需多少天?
(3)若按完成工作量的多少支付工资,甲装修公司应得多少元?

(1)求合作部分工作量y与工作时间x之间的函数关系式;
(2)完成此房屋装修共需多少天?
(3)若按完成工作量的多少支付工资,甲装修公司应得多少元?

解:(1)设合作部分一次函数的解析式是 (
( 是常数)
是常数)
由待定系数法解得 .
.
 合作部分一次函数的表达式为
合作部分一次函数的表达式为
(2)当 时,
时, ,解得
,解得
 完成此房屋装修共需9天
完成此房屋装修共需9天
(3)由正比例函数图象可知:甲的工作效率是
甲9天完成的工作量是:
 甲得到的工资是:
甲得到的工资是: (元)
(元)
 (
( 是常数)
是常数)由待定系数法解得
 .
. 合作部分一次函数的表达式为
合作部分一次函数的表达式为
(2)当
 时,
时, ,解得
,解得
 完成此房屋装修共需9天
完成此房屋装修共需9天 (3)由正比例函数图象可知:甲的工作效率是

甲9天完成的工作量是:

 甲得到的工资是:
甲得到的工资是: (元)
(元) (1)根据图象可设函数关系式为: (
( 是常数),然后利用待定系数法可以求出一次函数关系式;
是常数),然后利用待定系数法可以求出一次函数关系式;
(2)当 时,即可求出完成此房屋装修共需的天数;
时,即可求出完成此房屋装修共需的天数;
(3)先由正比例函数图象得到甲的工作效率,从而得到甲的工作量,即可得到工资总数。
 (
( 是常数),然后利用待定系数法可以求出一次函数关系式;
是常数),然后利用待定系数法可以求出一次函数关系式;(2)当
 时,即可求出完成此房屋装修共需的天数;
时,即可求出完成此房屋装修共需的天数;(3)先由正比例函数图象得到甲的工作效率,从而得到甲的工作量,即可得到工资总数。

练习册系列答案
相关题目

 (k≠0)的图像经过(1,2),则这个函数的图像一定经过点( )
(k≠0)的图像经过(1,2),则这个函数的图像一定经过点( )



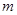 <0
<0