题目内容
已知:直角梯形ABCD中,DC⊥BC,AD∥BC,AD=AB=5,BC=8.动点P以1个单位/秒的速度从C开始,沿C—D—A方向运动,到达点A时停止.
(1)设△BCP的面积为y,运动的时间为t秒. 求y关于t的函数关系式,并写出t的范围;

(2)连接AP,当点P在CD上时,求在第几秒时,△ABP的面积与△BCP的面积相等?

(3)若在点P从点C出发的同时,另一动点M从A开始沿着A—D—C方向运动,运动速度为2个单位/秒. 求当P、M相遇时,△BCP的面积?
(1)设△BCP的面积为y,运动的时间为t秒. 求y关于t的函数关系式,并写出t的范围;

(2)连接AP,当点P在CD上时,求在第几秒时,△ABP的面积与△BCP的面积相等?

(3)若在点P从点C出发的同时,另一动点M从A开始沿着A—D—C方向运动,运动速度为2个单位/秒. 求当P、M相遇时,△BCP的面积?

(1)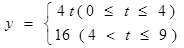 (2)
(2)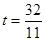 (3)12
(3)12
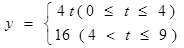 (2)
(2)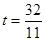 (3)12
(3)12解:(1)△BCP的面积y与运动时间t的关系:
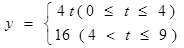
(2)△ABP的面积为: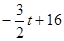 (0≤t≤4)
(0≤t≤4)
由于△ABP的面积=△BCP的面积,
得: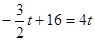 ,解得:
,解得: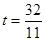 ,满足0≤t≤4;
,满足0≤t≤4;
答:在第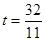 秒时,△ABP的面积等于△BCP的面积为
秒时,△ABP的面积等于△BCP的面积为
(3)设点M与点P的相遇时间为t ,由图形知:
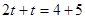 ,解得:
,解得: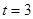 ,
,
将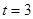 代入
代入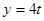 中,得:
中,得:
三角形BCP的面积y=12,
答:当P、M相遇时,△BCP的面积是12.
此题主要考查了学生对梯形性质及面积的掌握和对运动中问题的解决能力.
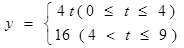
(2)△ABP的面积为:
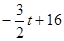 (0≤t≤4)
(0≤t≤4)由于△ABP的面积=△BCP的面积,
得:
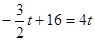 ,解得:
,解得: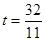 ,满足0≤t≤4;
,满足0≤t≤4;答:在第
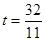 秒时,△ABP的面积等于△BCP的面积为
秒时,△ABP的面积等于△BCP的面积为(3)设点M与点P的相遇时间为t ,由图形知:
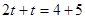 ,解得:
,解得: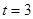 ,
,将
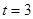 代入
代入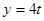 中,得:
中,得:三角形BCP的面积y=12,
答:当P、M相遇时,△BCP的面积是12.
此题主要考查了学生对梯形性质及面积的掌握和对运动中问题的解决能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目


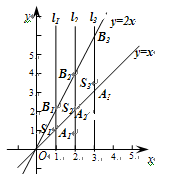

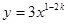 为反比例函数,则一次函数
为反比例函数,则一次函数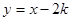 不经过第______象限.
不经过第______象限.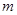 <0
<0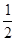
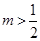
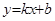 的图象如右图所示,则k、b的值为( )
的图象如右图所示,则k、b的值为( )