题目内容
【题目】(1)(阅读理解)
如图(1),AD是△ABC的中线,作△ABC的高AH.
∵AD是△ABC的中线
∴BD=CD
∵S△ABD=![]() BDAH,S△ACD=
BDAH,S△ACD=![]() CDAH
CDAH
∴S△ABD S△ACD(填:<或>或=)
(2)(结论拓展)
△ABC中,D是BC边上一点,若![]() ,则
,则![]() =
=
(3)(结论应用)
如图(3),请你将△ABC分成4个面积相等的三角形(画出分割线即可)
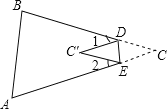
如图(4),BE是△ABC的中线,F是AB边上一点,连接CF交BE于点O,若![]() ,则
,则![]() = .说明你的理由
= .说明你的理由
【答案】(1)=;(2)![]() ;(3)3.
;(3)3.
【解析】
(1)结合中线的定义,根据等底同高的两个三角形面积相等可得结论;
(2)同理计算两三角形面积,并计算比值可得结论;
(3)根据三角形中线、中位线的性质可以解决分成4个面积相等的三角形问题.
如图4,连接AO,先根据三角形的中线平分三角形的面积得:S△ABE=S△CBE,S△AOE=S△COE,由差可得S△ABO=S△CBO,由同高三角形面积的比等于对应底边的比,可得结论.
解:(1)∵AD是△ABC的中线,
∴BD=CD,
∵S△ABD=![]() BDAH,S△ACD=
BDAH,S△ACD=![]() CDAH
CDAH
∴S△ABD=S△ACD,
故答案为:=;
(2)如图2,过A作AH⊥BC于H,

∵S△ABD=![]() BDAH,S△ACD=
BDAH,S△ACD=![]() CDAH,
CDAH,
 ,
,
故答案为:![]() ;
;
(3)如下图:
将△ABC的面积四等分的方法如图所示,(方法见图中说明)

如图4,结论:![]() =3;
=3;
理由是:如图4,连接AO,

∵BE是△ABC的中线,
∴S△ABE=S△CBE,S△AOE=S△COE,
∴S△ABO=S△CBO,
∵![]() ,
,
∴![]() ,
,
设S△BFO=x,则S△AFO=2x,S△CBO=3x,
![]() ,
,
![]() .
.
故答案为:3.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目