Question

【题目】如果一个角的两边与另一个角的两边分别平行，某同学为了探究这两个角的关系，画出来以下两个不同的图形，请你根据图形完成以下问题：

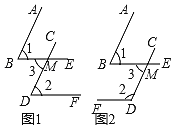
（1）如图1，如果AB∥CD，BE∥DF，那么∠1与∠2的关系是　 　；

如图2，如果AB∥CD，BE∥DF，那么∠1与∠2的关系是　 　；

（2）根据（1）的探究过程，我们可以得到结论：如果一个角的两边与另一个角的两边分别平行，那么这两个角的关系是　 　；

（3）利用结论解决问题：如果有两个角的两边分别平行，且一个角比另一个角的3倍少40°，则这两个角分别是多少度？

Answer 1

【答案】（1）相等，互补；（2）相等或互补；（3）20°，20°或55°，125°．

【解析】

（1）根据平行线的性质推出即可；
（2）根据（1）的结论得出即可；
（3）先得出方程，再求出方程的解即可．

解：（1）∵AB∥CD，BE∥DF，

∴∠1＝∠3，∠2＝∠3，

∴∠1＝∠2，

即∠1与∠2的关系是相等，

图2中∵AB∥CD，BE∥DF，

∴∠1＝∠3，∠2+∠3＝180°，

∴∠1+∠2＝180°，

即∠1与∠2的关系是互补，

故答案为：相等，互补；

（2）如果一个角的两边与另一个角的两边分别平行，那么这两个角的关系是相等或互补，故答案为：相等或互补；

（3）设两个角为x°和2x°﹣40°，

∵有两个角的两边分别平行，且一个角比另一个角的3倍少40°，

∴x＝3x﹣40或x+3x﹣40＝180，

解得：x＝20或x＝55，

即这两个角为20°，20°或55°，125°．