题目内容
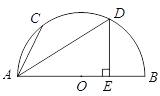
【题目】如图，C、D两点在以AB为直径的半圆O上，AD平分∠BAC，AB＝20，AD＝4
，DE⊥AB于E．
（1）求DE的长．
（2）求证：AC＝2OE．
【答案】（1）DE的长为4
；
（2）证明见解析.
【解析】解：（1）连接BD．∵AB为直径，∴∠ADB＝90°，
在Rt△ADB中，BD＝
＝
＝4
，∵S△ADB＝
AD·BD＝
AB·DE
∴AD·BD＝AB·DE，∴DE＝
＝
＝4
，
即DE＝4
（2）证明：连接OD，作OF⊥AC于点F．
∵OF⊥AC，∴AC＝2AF，∵AD平分∠BAC，∴∠BAC＝2∠BAD．
又∵∠BOD＝2∠BAD，∴∠BAC＝∠BOD，
Rt△OED和Rt△AFO中，∵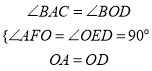
∴△AFO≌△OED（AAS），∴AF＝OE，∵AC＝2AF，∴AC＝2OE．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
